Mikroökonomie
Vorlesung 5

Prof. Frank Pisch PhD

Einführung

Motivation: Marktversagen

Die meisten Märkte funktionieren nicht wie unser benchmark und es kommt zu Marktversagen

Marktmacht (heute)
Externalitäten und öffentliche Güter
Unvollständige und asymmetrische Information
Menschliches Verhalten

Motivation: Marktmacht

Das erste und einfachste Marktversagen ist die Existenz von Marktmacht

Einzelne Unternehmen dominieren einen ganzen Markt

ASML für EUV Etchers, Google für Suchmaschinen, die DB InfraGO für das Bahnnetz etc.

Oft sind es wenige Unternehmen, die einen Markt unter sich aufteilen und hochstrategisch interagieren

Airbus vs Boeing, Coke vs Pepsi, Smartphones, Ölproduzenten

Marktmacht ermöglicht Unternehmen zudem, besondere Preistrategien zu nutzen und Märkte zu verzerren

Studentenpreise im Kino, Flugtickets, Drucker und Patronen, In-game purchases oder Entritt in Vergnügungsparks etc.

Ein Grund für Marktmacht ist oft eine aktive Abgrenzung von Wettbewerbern durch Design (z.B. Autos, Smartphones)

Überblick und Resourcen

Ziele

Monopole und ihre Wohlfahrtseffekte verstehen
Eingeschränkten Wettbewerb, also Oligopolsituationen verstehen und analysieren
Preissetzungsstrategien von Unternehmen analysieren und anwenden
Produktdifferenzierung als Grund für Marktmacht kennenlernen und verstehen

Ressourcen

Kapitel im Varian: 25, 26, 28

YouTube, ChatGPT

Monopolverhalten und Wohlfahrt

Entstehung von Monopolen

Teamarbeit:

Nennen Sie Beispiele für (quasi-)Monopolstellungen
Erklären Sie, warum es zu dieser Marktstruktur gekommen ist

Typische Situationen

Temporäre Technologievorsprünge
Natürliche Monopole (insbes. Netzwerkgüter): Je größer, desto niedrigere Durchschnittskosten
Patente und anderweitig geschütztes Wissen
Kartellverhalten aller Unternehmen

Das Gewinnmaximierungsproblem

Märkte, auf denen nur ein einziges Unternehmen aktiv ist, sind Monopolmärkte

Das Unternehmen antizipiert, dass eine Mengenverknappung zu höheren Preisen führt (oder dass die Nachfrage trotz höherer Preise nicht sofort vollständig einbricht)
Monopolisten können Preise oberhalb der Grenzkosten setzen und positive Gewinne abschöpfen
Hierfür nehmen wir an, dass es ausreichend hohe Markteintrittsbarrieren gibt

Das Gewinnmaximierungsproblem ist

\[ \text{max}_y \ \ \underbrace{p(y)y}_{Erlös} - c(y) \]

wobei der Erlös auch mit \(r(y)\equiv p(y)y\) bezeichnet wird und \(p(y)\) die Nachfragefunktion darstellt

Optimalitätsbedingung

Der Monopolist wählt genau die Menge \(y^{*,M}\), die Grenzkosten und Grenzerlös gleichsetzt

\[ \left. \frac{\mathrm{d} \ p(y)y}{\mathrm{d} y} \right |_{y^{*,M}} = \left. \frac{\mathrm{d} c(y)}{\mathrm{d} y} \right |_{y^{*,M}} \ \ \Leftrightarrow \ \ MR(y^{*,M})=MC(y^{*,M}) \]

Wäre \(MR>MC\), sollte die Menge ausgeweitet werden (und vice versa)

Der Grenzerlös setzt sich folgendermaßen zusammen (Kettenregel):

\[ MR(y) = \frac{\mathrm{d}y}{\mathrm{d}y}p(y) + \frac{\mathrm{d}p(y)}{\mathrm{d}y}y = p(y) + \frac{\mathrm{d}p(y)}{\mathrm{d}y}y \]

Beispiel: Lineare Nachfrage

Zur Veranschaulichung nehmen wir eine lineare Nachfragefunktion

\[ p(y) = a - b y \ \ \ \ \text{mit} \ \ a,b > 0 \]

Der Grenzerlös im Monopol ist

\[ MR^M(y) = \frac{\mathrm{d}}{\mathrm{d} y} \ (ay-by^2) = a-2by \]

Mit einer Kostenfunktion \(c(y)=c+dy^2\) und \(c,d >0\) haben wir eine Grenzkostenfunktion

\[ MC(y) = \frac{\mathrm{d}}{\mathrm{d}y} \ (c+dy^2) = 2dy \]

Monopolgleichgewicht mit linearer Nachfrage

Die optimale Menge ist kleiner als unter vollständigem Wettbewerb (bitte verifizieren):

\[ a-2by^{*,M} = 2dy^{*,M} \ \Leftrightarrow \ y^{*,M} = \frac{a}{2(b+d)} < \frac{a}{b+2d} = y^{*,W} \]

Der Marktpreis ist höher als unter vollständigem Wettbewerb

\[ p(y^{*,M}) = \frac{a(b+2d)}{2(b+d)}>\frac{2ad}{b+2d} = p(y^{*,W}) \]

Der Gewinn ist \[ \pi^{*,M} = \frac{a^2(b+2d)}{4(b+d)^2} \]

Diagramm: Monopolverhalten bei linearer Nachfrage

#| standalone: true
#| viewerHeight: 600

library(shiny)
library(shinydashboard)
library(ggplot2)
library(graphics)
library(ggpattern)
library(dplyr)
library(purrr)
library(bslib)
library(bs4Dash)




ui <- fluidPage(
  
  
  sidebarLayout(
    sidebarPanel(
      tabsetPanel(
        tabPanel(h5("Einstellungen"),
                 br(),
                 checkboxInput("mc", "Grenzkosten anzeigen", value = FALSE),
                 
                 checkboxInput("dem", "Inverse Nachfrage anzeigen", value = FALSE),
                 
                 checkboxInput("mr", "Grenzerlös anzeigen", value = FALSE),
                 
                 
                 
                
                 #h6(withMathJax("$$MC(y) = 2dy, p(y) = a - by$$")),
                 withMathJax(h6("\\(MC(y) = 2dy\\) und \\(p(y) = a - by\\)")),
                 
                 #h6(withMathJax("$$MC(y) = 2dy$$")," and ", withMathJax("$$p(y) = a - by$$")),
                 
                 
                 
                 sliderInput("a", "Parameter a", min = 1, max = 150, value = 80, step = 0.5),
                 sliderInput("b", "Parameter b", min = 0.1, max = 5, value = 1, step = 0.1),
                 sliderInput("d", "Parameter d", min = 0.1, max = 5, value = 1, step = 0.1),
                 
                 
                 
                 #h6(withMathJax("$$MC(y) = 2dy$$")),
                 #h6(withMathJax("$$MR(y) = a -2by$$")),
                 #h6(withMathJax("$$p(y) = a - by$$")),
                 
                 actionButton("reset", "Reset")
        ),
        
        
        
        tabPanel(h5("Wohlfahrt"),
                 checkboxInput("cs", "Konsumentenrente anzeigen", value = FALSE),
                 
                 checkboxInput("ps", "Produzentenrente anzeigen", value = FALSE),
                 
                 checkboxInput("wv", "Wohlfahrtsverlust anzeigen", value = FALSE),
                 
                 
                 
                 br(),
                 
                 uiOutput('kons_r'))
      )
      ),
    mainPanel(align = "center", plotOutput(outputId = "ggwplot", height = "500px", width = "600px")
    )
  )
)








server <- function(input, output, session) {
  
  g_kost <- function(d, y) {
    
    m_c <- 2 * d * y
    
    return(m_c)
  }
  
  nachfrage <- function(a, b, y){
    
    p_d <- a - b*y
    
    return(p_d)
    
  }
  
  g_erlös <- function(a, b, y){
    
    m_r <- a - 2* b*y
    
    return(m_r)
  }
  
  opt <- function(a,b,d) {
    
    
    
    y_m_opt <- a/(2*(b+d))
    y_opt <- a / (b+ 2*d)
    
    p_m_opt <- (a*b + 2*a*d) / (2*b + 2*d)
    p_opt <- (2*a*d) / (b + 2*d)
    
    return(list(p_opt = p_opt, y_opt = y_opt, p_m_opt = p_m_opt, y_m_opt = y_m_opt))
  }
  
  
  
  
  
  
  
  
  observeEvent(list(input$cs,input$ps, input$wv, input$dem, input$mc, input$mr, input$a, input$b, input$c, input$d), {
    a <- input$a
    b <- input$b
    c <- input$c
    d <- input$d
    
    cs <- input$cs
    wv <- input$wv
    mr <- input$mr
    mc <- input$mc
    
    y_v <- seq(0, 150, by = 0.05)
    
    p_d <- nachfrage(a, b, y_v)
    m_c <- g_kost(d, y_v)
    m_r <- g_erlös(a, b, y_v)
    
    
    
      
      grid <- tibble(
        
        y_val = y_v,
        
        MC_k = m_c,
        
        MR_k = m_r,
        
        D = p_d
        
      )
      
      Ergebnisse <- opt(a, b, d)
      p_opt <- Ergebnisse$p_opt 
      y_opt <- Ergebnisse$y_opt
      y_m_opt <- Ergebnisse$y_m_opt
      p_m_opt <- Ergebnisse$p_m_opt
      
      
    
    
    output$ggwplot <- renderPlot({
      if (input$dem == TRUE && input$mr == TRUE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
        
        
        
      } else if (input$dem == TRUE && input$mr == TRUE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          
          )
        
      } else if (input$dem == TRUE && input$mr == FALSE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
        
      } else if (input$dem == FALSE && input$mr == TRUE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
        
      } else if (input$dem == TRUE && input$mr == FALSE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
      
      
      } 
      else if (input$dem == FALSE && input$mr == FALSE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
      } else if (input$dem == FALSE && input$mr == TRUE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
       }
        else if (input$dem == FALSE && input$mr == FALSE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = D), color = "white", size = 0.1) +
          coord_cartesian(xlim = c(-5, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # Adjust this as necessary to position the legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white"))
        }
      
      
      
      if (input$dem && input$mc && input$mr && !is.null(p_m_opt) && input$cs == TRUE ) {
        g_plot <- g_plot +
          geom_ribbon_pattern(data = grid %>% filter(y_val <= y_m_opt),
                              aes(x = y_val, ymin = p_m_opt, ymax = D, fill = "Konsumentenrente"),
                              pattern = "stripe", 
                              pattern_fill = "red", 
                              pattern_angle = 45, 
                              pattern_density = 0.3, 
                              pattern_spacing = 0.01, 
                              alpha = 0.3) 
        } 
      
      if (input$dem && input$mc && input$mr && !is.null(p_m_opt) && input$wv == TRUE) {
        g_plot <- g_plot +
          geom_ribbon(data = grid %>% filter(y_val >= y_m_opt & y_val <= y_opt),
                              aes(x = y_val, ymin = MC_k, ymax = D, fill = "Wohlfahrtsverlust"))
                              
                             
      } 
      
      p_h <- g_erlös(a, b, y_m_opt)
       
      if (input$dem && input$mc && input$mr && !is.null(p_m_opt) && input$ps == TRUE) {
        g_plot <- g_plot +
          geom_ribbon_pattern(data = grid %>% filter(y_val <= y_m_opt),
                              aes(x = y_val, ymin = MC_k, ymax = p_m_opt, fill = "Produzentenrente"),
                              pattern = "circle", 
                              pattern_fill = "green", 
                              pattern_angle = 135, 
                              pattern_density = 0.3, 
                              pattern_spacing = 0.01, 
                              alpha = 0.3) 
      } 
      
      
      label1 <- bquote(p[M] ~ "≈")
      label2 <- bquote(p[W] ~ "≈")
      label3 <- bquote(y[M] ~ "≈")
      
    
      
      if (input$dem == TRUE && input$mr == TRUE && input$mc == TRUE) {
        g_plot <- g_plot +
          geom_segment(aes(x = y_m_opt, xend = y_m_opt, y = 0, yend = p_m_opt), color = "purple", linetype = "longdash", size = 0.7) +
          geom_segment(aes(x = 0, xend = y_m_opt, y = p_m_opt, yend = p_m_opt), color = "purple", linetype = "longdash", size = 0.7) +
          geom_segment(aes(x = 0, xend = y_opt, y = p_opt, yend = p_opt), color = "purple", linetype = "longdash", size = 0.7) +
          annotate("text", x = y_m_opt, y = 0, label = as.expression(bquote(.(label3) ~ .(round(y_m_opt)))), vjust = 1, hjust = 0.5, color = "purple", size = 5) +
          annotate("text", x = 0, y = p_m_opt, label = as.expression(bquote(.(label1) ~ .(round(p_m_opt)))), vjust = 0.5, hjust = 1, color = "purple", size = 5) +
          annotate("text", x = 0, y = p_opt, label = as.expression(bquote(.(label2) ~ .(round(p_opt)))), vjust = 0.5, hjust = 1, color = "purple", size = 5)
      }
      
      
      g_plot <- g_plot +
        scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange"), name = "Kurven") +
        scale_fill_manual(values = c("Konsumentenrente" = "#FF9999", "Wohlfahrtsverlust" = "black", "Produzentenrente" = "#ABCD00"), name = "") +
        guides(color = guide_legend(title = "Geraden", position = "bottom", title.position = "left", title.hjust = 1))
      
      
      
      
      
      print(g_plot) 
      
    })

  })  
  
  
  
  observeEvent(input$reset, {
    updateSliderInput(inputId = "a", value = 80)
    updateSliderInput(inputId = "b", value = 1)
    updateSliderInput(inputId = "c", value = 1)
    updateSliderInput(inputId = "d", value = 1)
    
    
    updateCheckboxInput(inputId = "cs", value = FALSE)
    updateCheckboxInput(inputId = "wv", value = FALSE)
    updateCheckboxInput(inputId = "ps", value = FALSE)
    
  })
  
  
  kons_r <- reactiveVal(0)
  wohl_v <- reactiveVal(0)
  prod_r <- reactiveVal(0)
  
  observeEvent(list(input$cs, input$ps, input$wv, input$m_c, input$m_r, input$dem, input$a, input$b, input$c, input$d), {
    a <- input$a
    b <- input$b
    c <- input$c
    d <- input$d
    
    
    Ergebnisse <- opt(a, b, d)
    p_opt <- Ergebnisse$p_opt
    y_opt <- Ergebnisse$y_opt
    y_m_opt <- Ergebnisse$y_m_opt
    p_m_opt <- Ergebnisse$p_m_opt
    
    p_dem_null <- nachfrage(a, b, 0) 
    
    if (input$dem && input$mc && input$mr && input$cs) {
   
      kons_r((p_dem_null - p_m_opt) * (y_m_opt))
      
   
    }
   if (input$dem && input$mc && input$mr && input$wv) {
     wohl_v((p_m_opt - p_opt) * (y_opt - y_m_opt) + (p_opt - 2*d*y_m_opt) * (y_opt - y_m_opt))
   }
    
    p_h <- g_erlös(a, b, y_m_opt)
    
    
    if (input$dem && input$mc && input$mr && input$ps) {
      prod_r((p_m_opt - p_h)* y_m_opt + (p_h * y_m_opt)/2)
    }
  
  output$kons_r <- renderUI({
    
    kons_r_r <- round(kons_r(), digits = 2)
    prod_r_r <- round(prod_r(), digits = 2)
    wohl_v_r <- round(wohl_v(), digits = 2)
    
    
    withMathJax(HTML(paste("Konsumentenrente:", kons_r_r, "<br>", "Produzentenrente:", prod_r_r , "<br>", "Wohlfahrtsverlust:", wohl_v_r, "<br>")))
    })
  })
  
  
  
}

shinyApp(ui = ui, server = server)

Komparative Statik im Monopol

Teamarbeit: Gehen Sie zurück zur vorherigen Folie und

reduzieren Sie die Nachfrage
machen Sie die Nachfrage elastischer
erhöhen Sie die Grenzkosten – entsprechen die Veränderungen Ihren Erwartungen?

Preissetzung im vollständigen Wettbewerb

Die Optimalitätsbedingung des Monopolisten kann umgeformt werden zu

\[ MC(y^*) = p(y^*) \left [1+ \left. \frac{\mathrm{d}p(y)}{\mathrm{d}y} \right |_{y^*} \ \ \ \frac{y^*}{p(y^*)} \right] = p(y^*) \left[1-\frac{1}{|\varepsilon_{y,p}(y^*)|} \right] \\ \]

Im vollständigen Wettbewerb ist die residuale Nachfrage – die Nachfrage für ein einzelnes Unternehmen – komplett elastisch: \(|\varepsilon_{y,p}(y)|\rightarrow\infty\)

es gilt “Preis gleich Grenzkosten”

Preissetzung im Monopol

Die residuale Nachfrage für einen Monopolisten ist weniger elastisch

Er verlangt daher einen Aufschlag auf die Grenzkosten

\[ p(y^*) = \underbrace{\frac{|\varepsilon_{y,p}|}{|\varepsilon_{y,p}|-1}}_{Aufschlag} MC(y^*) \]

Je unelastischer die Nachfrage – je niedriger \(|\varepsilon_{y,p}|\) – desto höher der Aufschlag
Der Monopolist wird aber nie im unelastischen Bereich (\(|\varepsilon_{y,p}|<1\)) anbieten, da der Grenzerlös negativ wäre

Ineffizienz des Monopols

Zur Erinnerung:

Vollständiger Wettbewerb führt zu Pareto-Effizienz, da das Gut zu tatsächlichen Kosten konsumiert wird

Im Monopol liegt der Preis über den Grenzkosten, sodass einige Personen nicht konsumieren können, obwohl ihre Zahlungsbereitschaft über den Produktionskosten liegt

Könnte der Monopolist diese Einheiten produzieren und diesen Nicht-Käufern zu einem günstigeren Preis oberhalb der Grenzkosten anbieten, hätten wir eine Pareto-Verbesserung

Dann würden aber infra-marginale Konsumenten einen höheren Preis zahlen und wir schließen dies zunächst aus (sog. Preisdiskriminierung)

Somit ist das Monopol ineffizient!

Diagramm: Wohlfahrt im Monopol bei linearer Nachfrage

#| standalone: true
#| viewerHeight: 600

library(shiny)
library(shinydashboard)
library(ggplot2)
library(graphics)
library(ggpattern)
library(dplyr)
library(purrr)
library(bslib)
library(bs4Dash)




ui <- fluidPage(
  
  
  sidebarLayout(
    sidebarPanel(
      tabsetPanel(
        tabPanel(h5("Einstellungen"),
                 br(),
                 checkboxInput("mc", "Grenzkosten anzeigen", value = FALSE),
                 
                 checkboxInput("dem", "Inverse Nachfrage anzeigen", value = FALSE),
                 
                 checkboxInput("mr", "Grenzerlös anzeigen", value = FALSE),
                 
                 
                 
                
                 #h6(withMathJax("$$MC(y) = 2dy, p(y) = a - by$$")),
                 withMathJax(h6("\\(MC(y) = 2dy\\) und \\(p(y) = a - by\\)")),
                 
                 #h6(withMathJax("$$MC(y) = 2dy$$")," and ", withMathJax("$$p(y) = a - by$$")),
                 
                 
                 
                 sliderInput("a", "Parameter a", min = 1, max = 150, value = 80, step = 0.5),
                 sliderInput("b", "Parameter b", min = 0.1, max = 5, value = 1, step = 0.1),
                 sliderInput("d", "Parameter d", min = 0.1, max = 5, value = 1, step = 0.1),
                 
                 
                 
                 #h6(withMathJax("$$MC(y) = 2dy$$")),
                 #h6(withMathJax("$$MR(y) = a -2by$$")),
                 #h6(withMathJax("$$p(y) = a - by$$")),
                 
                 actionButton("reset", "Reset")
        ),
        
        
        
        tabPanel(h5("Wohlfahrt"),
                 checkboxInput("cs", "Konsumentenrente anzeigen", value = FALSE),
                 
                 checkboxInput("ps", "Produzentenrente anzeigen", value = FALSE),
                 
                 checkboxInput("wv", "Wohlfahrtsverlust anzeigen", value = FALSE),
                 
                 
                 
                 br(),
                 
                 uiOutput('kons_r'))
      )
      ),
    mainPanel(align = "center", plotOutput(outputId = "ggwplot", height = "500px", width = "600px")
    )
  )
)








server <- function(input, output, session) {
  
  g_kost <- function(d, y) {
    
    m_c <- 2 * d * y
    
    return(m_c)
  }
  
  nachfrage <- function(a, b, y){
    
    p_d <- a - b*y
    
    return(p_d)
    
  }
  
  g_erlös <- function(a, b, y){
    
    m_r <- a - 2* b*y
    
    return(m_r)
  }
  
  opt <- function(a,b,d) {
    
    
    
    y_m_opt <- a/(2*(b+d))
    y_opt <- a / (b+ 2*d)
    
    p_m_opt <- (a*b + 2*a*d) / (2*b + 2*d)
    p_opt <- (2*a*d) / (b + 2*d)
    
    return(list(p_opt = p_opt, y_opt = y_opt, p_m_opt = p_m_opt, y_m_opt = y_m_opt))
  }
  
  
  
  
  
  
  
  
  observeEvent(list(input$cs,input$ps, input$wv, input$dem, input$mc, input$mr, input$a, input$b, input$c, input$d), {
    a <- input$a
    b <- input$b
    c <- input$c
    d <- input$d
    
    cs <- input$cs
    wv <- input$wv
    mr <- input$mr
    mc <- input$mc
    
    y_v <- seq(0, 150, by = 0.05)
    
    p_d <- nachfrage(a, b, y_v)
    m_c <- g_kost(d, y_v)
    m_r <- g_erlös(a, b, y_v)
    
    
    
      
      grid <- tibble(
        
        y_val = y_v,
        
        MC_k = m_c,
        
        MR_k = m_r,
        
        D = p_d
        
      )
      
      Ergebnisse <- opt(a, b, d)
      p_opt <- Ergebnisse$p_opt 
      y_opt <- Ergebnisse$y_opt
      y_m_opt <- Ergebnisse$y_m_opt
      p_m_opt <- Ergebnisse$p_m_opt
      
      
    
    
    output$ggwplot <- renderPlot({
      if (input$dem == TRUE && input$mr == TRUE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
        
        
        
      } else if (input$dem == TRUE && input$mr == TRUE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          
          )
        
      } else if (input$dem == TRUE && input$mr == FALSE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
        
      } else if (input$dem == FALSE && input$mr == TRUE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
        
      } else if (input$dem == TRUE && input$mr == FALSE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = D, color = "Nachfrage"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
      
      
      } 
      else if (input$dem == FALSE && input$mr == FALSE && input$mc == TRUE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MC_k, color = "Grenzkosten"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
      } else if (input$dem == FALSE && input$mr == TRUE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = MR_k, color = "Grenzerlös"), size = 1.3) +
          scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange")) +
          guides(color = guide_legend(title = "Kurven", position = "bottom", title.position = "left", title.hjust = 0.5)) +
          
          coord_cartesian(xlim = c(-10, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # position -> legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white")
          )
       }
        else if (input$dem == FALSE && input$mr == FALSE && input$mc == FALSE) {
        
        g_plot <- ggplot(grid) +
          geom_line(aes(x = y_val, y = D), color = "white", size = 0.1) +
          coord_cartesian(xlim = c(-5, 100), ylim = c(-5, 100)) +
          theme_minimal() +
          labs(x = "Menge y", y = "Preis p") +
          theme(
            axis.text = element_text(size = 14),
            axis.title = element_text(size = 16),
            plot.title = element_text(size = 20),
            legend.position = c(0.9, 0.9),  # Adjust this as necessary to position the legend
            legend.justification = c(0.5, 0.5),  # Top right corner
            legend.background = element_rect(fill = "white", color = "black"),
            legend.key = element_rect(fill = "white", color = "white"))
        }
      
      
      
      if (input$dem && input$mc && input$mr && !is.null(p_m_opt) && input$cs == TRUE ) {
        g_plot <- g_plot +
          geom_ribbon_pattern(data = grid %>% filter(y_val <= y_m_opt),
                              aes(x = y_val, ymin = p_m_opt, ymax = D, fill = "Konsumentenrente"),
                              pattern = "stripe", 
                              pattern_fill = "red", 
                              pattern_angle = 45, 
                              pattern_density = 0.3, 
                              pattern_spacing = 0.01, 
                              alpha = 0.3) 
        } 
      
      if (input$dem && input$mc && input$mr && !is.null(p_m_opt) && input$wv == TRUE) {
        g_plot <- g_plot +
          geom_ribbon(data = grid %>% filter(y_val >= y_m_opt & y_val <= y_opt),
                              aes(x = y_val, ymin = MC_k, ymax = D, fill = "Wohlfahrtsverlust"))
                              
                             
      } 
      
      p_h <- g_erlös(a, b, y_m_opt)
       
      if (input$dem && input$mc && input$mr && !is.null(p_m_opt) && input$ps == TRUE) {
        g_plot <- g_plot +
          geom_ribbon_pattern(data = grid %>% filter(y_val <= y_m_opt),
                              aes(x = y_val, ymin = MC_k, ymax = p_m_opt, fill = "Produzentenrente"),
                              pattern = "circle", 
                              pattern_fill = "green", 
                              pattern_angle = 135, 
                              pattern_density = 0.3, 
                              pattern_spacing = 0.01, 
                              alpha = 0.3) 
      } 
      
      
      label1 <- bquote(p[M] ~ "≈")
      label2 <- bquote(p[W] ~ "≈")
      label3 <- bquote(y[M] ~ "≈")
      
    
      
      if (input$dem == TRUE && input$mr == TRUE && input$mc == TRUE) {
        g_plot <- g_plot +
          geom_segment(aes(x = y_m_opt, xend = y_m_opt, y = 0, yend = p_m_opt), color = "purple", linetype = "longdash", size = 0.7) +
          geom_segment(aes(x = 0, xend = y_m_opt, y = p_m_opt, yend = p_m_opt), color = "purple", linetype = "longdash", size = 0.7) +
          geom_segment(aes(x = 0, xend = y_opt, y = p_opt, yend = p_opt), color = "purple", linetype = "longdash", size = 0.7) +
          annotate("text", x = y_m_opt, y = 0, label = as.expression(bquote(.(label3) ~ .(round(y_m_opt)))), vjust = 1, hjust = 0.5, color = "purple", size = 5) +
          annotate("text", x = 0, y = p_m_opt, label = as.expression(bquote(.(label1) ~ .(round(p_m_opt)))), vjust = 0.5, hjust = 1, color = "purple", size = 5) +
          annotate("text", x = 0, y = p_opt, label = as.expression(bquote(.(label2) ~ .(round(p_opt)))), vjust = 0.5, hjust = 1, color = "purple", size = 5)
      }
      
      
      g_plot <- g_plot +
        scale_color_manual(values = c("Grenzerlös" = "blue", "Nachfrage" = "red", "Grenzkosten" = "orange"), name = "Kurven") +
        scale_fill_manual(values = c("Konsumentenrente" = "#FF9999", "Wohlfahrtsverlust" = "black", "Produzentenrente" = "#ABCD00"), name = "") +
        guides(color = guide_legend(title = "Geraden", position = "bottom", title.position = "left", title.hjust = 1))
      
      
      
      
      
      print(g_plot) 
      
    })

  })  
  
  
  
  observeEvent(input$reset, {
    updateSliderInput(inputId = "a", value = 80)
    updateSliderInput(inputId = "b", value = 1)
    updateSliderInput(inputId = "c", value = 1)
    updateSliderInput(inputId = "d", value = 1)
    
    
    updateCheckboxInput(inputId = "cs", value = FALSE)
    updateCheckboxInput(inputId = "wv", value = FALSE)
    updateCheckboxInput(inputId = "ps", value = FALSE)
    
  })
  
  
  kons_r <- reactiveVal(0)
  wohl_v <- reactiveVal(0)
  prod_r <- reactiveVal(0)
  
  observeEvent(list(input$cs, input$ps, input$wv, input$m_c, input$m_r, input$dem, input$a, input$b, input$c, input$d), {
    a <- input$a
    b <- input$b
    c <- input$c
    d <- input$d
    
    
    Ergebnisse <- opt(a, b, d)
    p_opt <- Ergebnisse$p_opt
    y_opt <- Ergebnisse$y_opt
    y_m_opt <- Ergebnisse$y_m_opt
    p_m_opt <- Ergebnisse$p_m_opt
    
    p_dem_null <- nachfrage(a, b, 0) 
    
    if (input$dem && input$mc && input$mr && input$cs) {
   
      kons_r((p_dem_null - p_m_opt) * (y_m_opt))
      
   
    }
   if (input$dem && input$mc && input$mr && input$wv) {
     wohl_v((p_m_opt - p_opt) * (y_opt - y_m_opt) + (p_opt - 2*d*y_m_opt) * (y_opt - y_m_opt))
   }
    
    p_h <- g_erlös(a, b, y_m_opt)
    
    
    if (input$dem && input$mc && input$mr && input$ps) {
      prod_r((p_m_opt - p_h)* y_m_opt + (p_h * y_m_opt)/2)
    }
  
  output$kons_r <- renderUI({
    
    kons_r_r <- round(kons_r(), digits = 2)
    prod_r_r <- round(prod_r(), digits = 2)
    wohl_v_r <- round(wohl_v(), digits = 2)
    
    
    withMathJax(HTML(paste("Konsumentenrente:", kons_r_r, "<br>", "Produzentenrente:", prod_r_r , "<br>", "Wohlfahrtsverlust:", wohl_v_r, "<br>")))
    })
  })
  
  
  
}

shinyApp(ui = ui, server = server)

Wohlfahrt im Vergleich zum Benchmark

Wenn man das Monopol mit unserem benchmark vergleicht, sieht man folgende Effekte:

Konsument:innen, die weiter konsumieren, zahlen höhere Preise und verlieren an Konsumentenrente
Einige Konsument:innen werden aus dem Markt verdrängt und verlieren ihre gesamte Konsumentenrente
Der Monopolist eignet sich Renten der aktiven Konsument:innen an
Der Monopolist verliert bestimmte Renten, da einige Konsument:innen aufhören, zu konsumieren

Insgesamt gewinnt der Monopolist, die Konsument:innen verlieren, und es entsteht eine Ineffizienz, die die Gesamtwohlfahrt reduziert

Teamarbeit: Was ist wettbewerbsrechtlich zu tun?

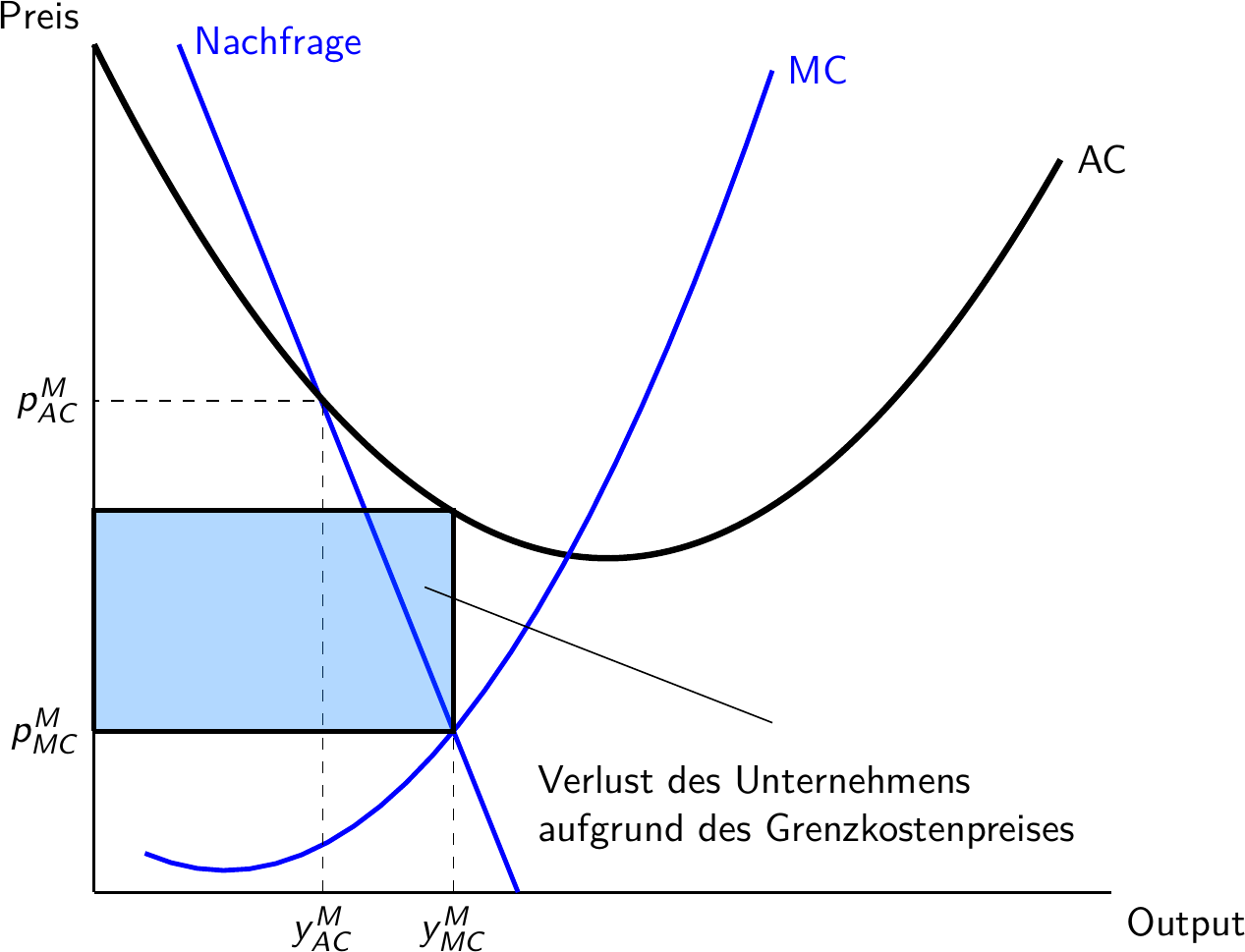
Spezialfall: Natürliches Monopol

Natürliche Monopole sind aus technologischen Gründen unvermeidbar, aber ineffizient

Die relevante Nachfrage liegt im Bereich fallender Durchschnittskosten - “big is beautiful”
Der Monopolist verknappt die Menge künstlich und zerstört Wohlfahrt

Der Staat könnte den Monopolisten zwingen, zu Grenzkosten anzubieten

Problem: Der Preis muss beim natürlichen Monopol unterhalb der Durchschnittkosten liegen (siehe Folie 20)
Der Monopolist macht Verluste und muss den Markt verlassen

Aus diesem Grund werden bestimmte Güter und Dienstleistungen von staatlicher Hand bereitgestellt

Netze wie Strom, Wasser, Verkehr

Grafik Natürliches Monopol

Oligopole

Übersicht

Bertrand Modell (Preiswettbewerb)
Cournot Modell (Mengenwettbewerb)
Stackelberg Modell (Dynamischer Wettbewerb)
Kartelle

Anwendung: Preiswettbewerb für Chips

Vergleichsportale führen in Märkten für ähnliche Produkte zu intensivem Preiswettbewerb

Ein Beispiel sind Computerteile wie RAM Module, CPUs etc. auf pricewatch.com

Ellison/Ellison (2009 ECTA) scrapen Daten in vier Kategorien über mehrere Monate und analysieren diese Märkte

Viele Anbieter von identischen Produkten, die nach aufsteigenden Preisen sortiert erscheinen
Nachfragen sind enorm elastisch: Eine Preiserhöhung um 1% führt zu einer Abnahme der Nachfrage um >20%!
Als Reaktion versuchen die Anbieter die Konsument:innen zu verwirren und den Wettbewerb zu schwächen

Was wäre ein gutes Modell, um die Interaktionen und Konsequenzen zu verstehen?

Das Bertrand Duopol

Annahmen

Zwei identische Firmen \(1,2\) mit Grenzkosten \(c\)
Nachfragefunktion (Gesamtnachfrage ist \(Q\))

\[ q_i(p_i, p_j) = \begin{cases} Q & \hspace{1.05cm} p_i < p_j, \\ \frac{Q}{2} & \text{falls } \ \ p_i = p_j, \\ 0 & \hspace{1.05cm} p_i > p_j. \end{cases} \]

Keine Kapazitätsbeschränkungen
Wettbewerb durch Preissetzung

Teamarbeit: Was ist das optimale Verhalten der beiden Firmen?

Das Bertrand Paradox

Die beste Antwort – oder auch Reaktionsfunktion – von Unternehmen \(i\) auf Preis \(p_j\) ist

\[ p_i^*(p_j) = \begin{cases} p_j - \varepsilon & \hspace{1.05cm} p_j > c \\ c & \text{falls } \ \ p_j = c, \\ [c,\infty) & \hspace{1.05cm} p_j < c. \end{cases} \]

wobei \(\varepsilon>0\) eine sehr kleine Einheit ist

Die Reaktionsfunktion hat eine positive Steigung: Eine Preiserhöhung des einen Unternehmens führt zu einer Preiserhöhung des anderen
Die Strategien sind somit strategische Komplemente

Im Gleichgewicht setzen also beide Unternehmen ihre Preise gleich den (identischen) Grenzkosten

Wäre \(p_j'=p_i'>c\), dann könnte eines der Unternehmen \(\varepsilon\) weniger verlangen, die gesamte Nachfrage befriedigen, und große Gewinne machen
Es gibt also immer eine einseitig attraktive Abweichung, solange die Preise über den Grenzkosten liegen

Dieses Ergebnis wird auch als Bertrand Paradox bezeichnet: Im Preiswettbewerb genügen zwei Unternehmen, um vollständigen Wettbewerb herzustellen

Auflösung des Bertrand Paradox

In der Realität sehen wir selten eine solch extreme Konkurrenz

Produktdifferenzierung
Unvollständige Information über Kosten der anderen Unternehmen
Kapazitätsbeschränkungen
Dynamischer Wettbewerb (siehe unten)
Etc.

Mengenwettbewerb: Kapazitätsbeschränkungen

Brander/Zhang (1990, RAND) betrachten die Luftfahrtindustrie in den USA

Auf vielen Routen gibt es zwei, maximal drei Anbieter
Flugzeuge, Slots in Flugplänen etc. müssen im Voraus geplant werden und Preise stellen sich aufgrund der Nachfrage und des Gesamtangebots ein
Einzelne Einheiten haben praktisch keine Grenzkosten

Die Autoren zeigen, dass diese Industrie am besten durch Wettbewerb in Mengen/Kapazitäten charakterisiert wird

Im Unterschied zu Bertrand ist die Residualnachfrage nicht perfekt elastisch
Wir nennen dieses Modell Cournot Modell

Andere Beispiele: Telekommunikation, Öl und andere extraktive Industrien, Elektrizität etc.

Das Cournot Modell

Annahmen

\(n\geq 2\) identische Firmen mit Grenzkosten \(c=0\)
Inverse Nachfragefunktion (\(Q=\sum_i^n q_i\))

\[ p = p \left (\sum_i^n q_i \right) = \underbrace{a-bQ}_{\text{Lineare Nachfrage}} \]

Alle Firmen akzeptieren den gleichen Preis, Wettbewerb durch Mengensetzung

Lösung des Cournot Duopols

Unternehmen maximieren Gewinne und nehmen die Menge des anderen als gegeben hin

\[ \mathrm{max}_{q_i} \ \ \ \pi_i = p(q_i, q_j^*) \ q_i = [a-b(q_i+q_j^*)]q_i \]

Die notwendige BeO ist die Reaktionsfunktion

\[ q_i^* = \frac{a-bq_j^*}{2b} \]

Die Steigung ist negativ: Auf eine Mengenerhöhung des einen Unternehmens reagiert das andere mit einer Mengensenkung um den Preis zu stabilisieren (Strategische Substitute)

Das Gleichgewicht liegt dort, wo sich die Reaktionsfunktionen schneiden, also bei \(q_i^*=q_j^*\)

\[ q_i^*=q_j^*=\frac{a}{3b} \]

Beide Unternehmen spielen ihre beste Antwort und wollen demnach nicht abweichen

Der Gleichgewichtspreis ist also \(p^*=a/3\), bei einer abgesetzten Menge von \(2a/3b\)

Vergleich: Bertrand vs Cournot

Im Monopol macht es keinen Unterschied, ob das Unternehmen den Preis oder die Menge setzt

Im Oligopol hängen die Marktergebnisse von der strategischen Variable ab

Im Cournot Wettbewerb sind die Mengen strategische Substitute; Im Bertrand Wettbewerb sind Preise strategische Komplemente
- Kann zur Charakterisierung von Märkten und zu wettbewerbspolischen Evaluation genutzt werden
Preiswettbewerb ist “härter”, da man im einfachsten Fall sogar ein voll effizientes Gleichgewicht erhält

Eine wichtige Determinante von Marktmacht ist also die Form des Wettbewerbs!

Dynamischer Wettbewerb

In vielen Märkten werden Entscheidungen nicht gleichzeitig, sondern sequenziell getroffen

Apple iPhone vs Samsung Galaxy
IBM und andere Unternehmen
Viele wiederholte Interaktionen

Fragen

Wie verändert sich das Marktergebnis?
Gibt es eine Vor- oder Nachteil, wenn man im Markt “führt”? Oder “folgt”?
Hängen die Erkenntnisse von der Art des Wettbewerbs ab?

Das Stackelberg Modell

Annahmen

Zwei Unternehmen \(1,2\) konkurrieren in Mengen
\(1\) setzt seine Menge zuerst (“Führer”), dann folgt \(2\) (“Folger”)
Grenzkosten sind \(c=0\)
Inverse Nachfragefunktion \(\left ( Q=\sum_i^n q_i \right )\)

\[ p = p \left (\sum_i^n q_i \right) = \underbrace{a-bQ}_{\text{Lineare Nachfrage}} \]

Alle Firmen akzeptieren den gleichen Preis

Heinrich Freiherr von Stackelberg, Wikipedia

Lösung des Stackelberg Spiels

Wie in jedem sequenziellen Spiel mit vollständiger Information bedienen wir uns der Rückwärtsinduktion, um ein teilspielperfektes Gleichgewicht zu finden

Zunächst lösen wir das Problem des Folgers gegeben eine allgemeine Menge des Führers; Wir finden also die Reaktionsfunktion

\[ \mathrm{max}_{q_2} \ \ \ p(q_1',q_2)\ q_2 \]

Dann lösen wir das Problem des Stackelberg-Führers; Dieser internalisiert die beste Antwort des Folgers

\[ \mathrm{max}_{q_1} \ \ \ p(q_1,q_2^*(q_1))\ q_1 \]

Stackelberg Lösung mit linearer Nachfrage

Mit linearer Nachfrage und Grenzkosten \(c=0\) ist die Reaktionsfunktion von \(2\)

\[ \mathrm{max}_{q_2} \ \ \ q_2 \ [a-b(q_1'+q_2)] \ \Rightarrow \ \ q_2^*(q_1') = \frac{a-bq_1'}{2b} \]

Der Stackelberg-Führer setzt also eine Menge

\[ \mathrm{max}_{q_1} \ \ \ q_1 \ [a-b(q_1+q_2^*(q_1))] =q_1 \ \left [a-b \left (q_1+\frac{a-bq_1}{2b} \right) \right] = \frac{a}{2}q_1 - \frac{b}{2} q_1^2 \ \Rightarrow \ \ q_1^* = \frac{a}{2b} \ \underbrace{(> \frac{a}{3b})}_{\text{Cournot}} \]

Der Folger spielt

\[ q_2^* = \frac{a}{4b} \ \underbrace{(<\frac{a}{3b})}_{\text{Cournot}} \]

Die Gleichgewichtsmenge ist mit \(3a/4b\) höher, der Preis von \(a/4\) niedriger als unter Cournot

Marktführer-Vorteil

Die Gleichgewichts-Gewinne sind

\[ \pi_1^* = \frac{a^2}{8b} \ (> \frac{a^2}{9b}=\pi^{Cournot}), \ \ \ \ \pi_2^* = \frac{a^2}{16b} \ (< \pi^{Cournot}) \]

Der Stackelberg-Führer flutet den Markt und macht große Gewinne, während sich der Folger einschränkt, um Preise zu stabilisieren

Dies ist eine direkte Konsequenz aus den Reaktionsfunktionen im Mengenwettbewerb
Es gibt also einen first-mover advantage

Das Vitamin-Kartell

Einer der größten Kartell-Fälle war das “Vitamin-Kartell” von Roche und BASF in den frühen 90er Jahren

Roche und BASF waren die größten Anbieter von Nahrungsergänzungsmitteln und Preise waren durch starken Wettbewerb niedrig
Wiederholte Treffen in der Schweiz und auch mit anderen Unternehmen (z.B. Merck), um die Märkte für Vitamine A, C, E u.a. aufzuteilen
Natürlicher Zusammenbruch von 6 Kartellen bis 1995, Auflösung der anderen ab 1999; Millionenstrafen ab 2003

Igami und Sugaya (2022, REStud) analysieren diesen Fall

Sie modellieren den Vitamin-Markt als Cournot-Wettbewerb und quantifizieren die Parameter
Das Vitamin C Kartell war instabil, da relative Netto-Gewinne durch Markteintritt und Nachfragewachstum fielen
Bei Vitamin A und E gab es weniger Markteintritt; erwartete Kartell-Gewinne waren höher als außerhalb des Kartells

Kartellverhalten im Duopol

Unternehmen im Cournot-Duopol schließen sich zusammen und verhalten sie sich wie ein Monopolist

Bei linearer Nachfrage und Grenzkosten \(c=0\) reduzieren sie die Menge auf

\[ y^{*,K}=\frac{a}{2b} < \frac{2a}{3b} = 2 \ y^{*,C} \]

Der Preis steigt auf

\[ p(y^{*,K}) = \frac{a}{2} > \frac{a}{3} = p(y^{*,C}) \]

Der Gewinn ist

\[ \pi^{*,K} = \frac{1}{2} \ \frac{a}{2b} \ \frac{a}{2} = \frac{a^2}{8b} > \frac{a^2}{9b} = \pi^{*,C} \]

Das Kartell im Cournot-Duopol führt zu höheren Gewinnen als im Wettbewerb, sodass es stabil ist

Teamarbeit: Wie hoch müssen Entdeckungswahrscheinlichkeit und Strafmaß sein, um das Kartell zu verhindern?

Exkurs: Stabilität eines bestehenden Kartells I

Ein Unternehmen will im Kartell bleiben, wenn die erwarteten Gewinne innerhalb höher sind als außerhalb

Nehmen wir an, dass bei einer einseitigen Abweichung von der abgesprochenen Menge in Zukunft immer (zur Strafe) Cournot gespielt wird

Die erwarteten Gewinne innerhalb des Kartells – bis in alle Ewigkeit – sind (Diskontierungsfaktor \(\delta \in (0,1)\))

\[ \pi^{*,K} + \sum_{s=1}^{\infty} \delta^s \ \pi^{*,K} = \frac{\pi^{*,K}}{1+\delta} \]

Die erwarteten Gewinne einer einseitigen Abweichung sind

\[ \pi^{*,A} + \sum_{s=1}^{\infty} \delta^s \ \pi^{*,C} = \pi^{*,A} + \frac{\delta \ \pi^{*,C}}{1+\delta} \]

Wie hoch ist \(\pi^{*,A}\)?

Exkurs: Stabilität eines bestehenden Kartells II

Die optimale Abweichungsmenge – gegeben dass Unternehmen 2 noch die Kartellmenge spielt – ist

\[ y^{*,A}_1 = \frac{3a}{8b} \ \ \ \ \ \left (\text{bei} \ \ y^{*,K}_2 = \frac{a}{4b} \right) \]

Beim Abweichungspreis von \(p(y^{*,A}_1+y^{*,K}_2)=3a/8\) sind die Gewinne

\[ \pi^{*,K}_2 = \frac{3a^2}{32b} \ \ \text{und} \ \ \pi^{*,A}_1 = \frac{9a^2}{64b} > \pi^{*,K}_2 \]

Man kann leicht ausrechnen, bei welchem Diskontfaktor \(\delta\) die Unternehmen indifferent sind

Ein bestehendes Kartell bleibt nur stabil, wenn die beteiligten Unternehmen ausreichend geduldig sind und der Markt nicht zu kompetitiv wird

Preisdiskriminierung

Motivation

Oft werden die gleichen Güter und Dienstleistungen nicht den gleichen Kund:innen zu gleichen Preisen angeboten

Autohändler passen Angebote stark auf einzelne Kunden an (Finanzierung, Nachlässe, in Zahlung geben etc.)
Viele Unternehmen geben Mengenrabatte (z.B. Strom, Gastronomie)
Studentenrabatte, Seniorenrabatte (z.B. Museen, Theater, Gastronomie)

Voraussetzungen:

Marktmacht des Unternehmens
Keine Arbitrage (im Gegensatz zum einfachen Monopol)

Preisdiskriminierung Ersten Grades

Der Monopolist verkauft den gleichen Output zu unterschiedlichen Preisen an unterschiedliche Konsument:innen

Er kann Konsument:innen nach Zahlungsbereitschaft trennen und verlangt immer den höchstmöglichen Preis
Wird auch als perfekte Preisdiskriminierung bezeichnet und ist ein Fall direkter Preisdiskriminierung
Beispiele sind sehr selten (“name-your-own-price”?)

Diagramm: Perfekte Preisdiskriminierung

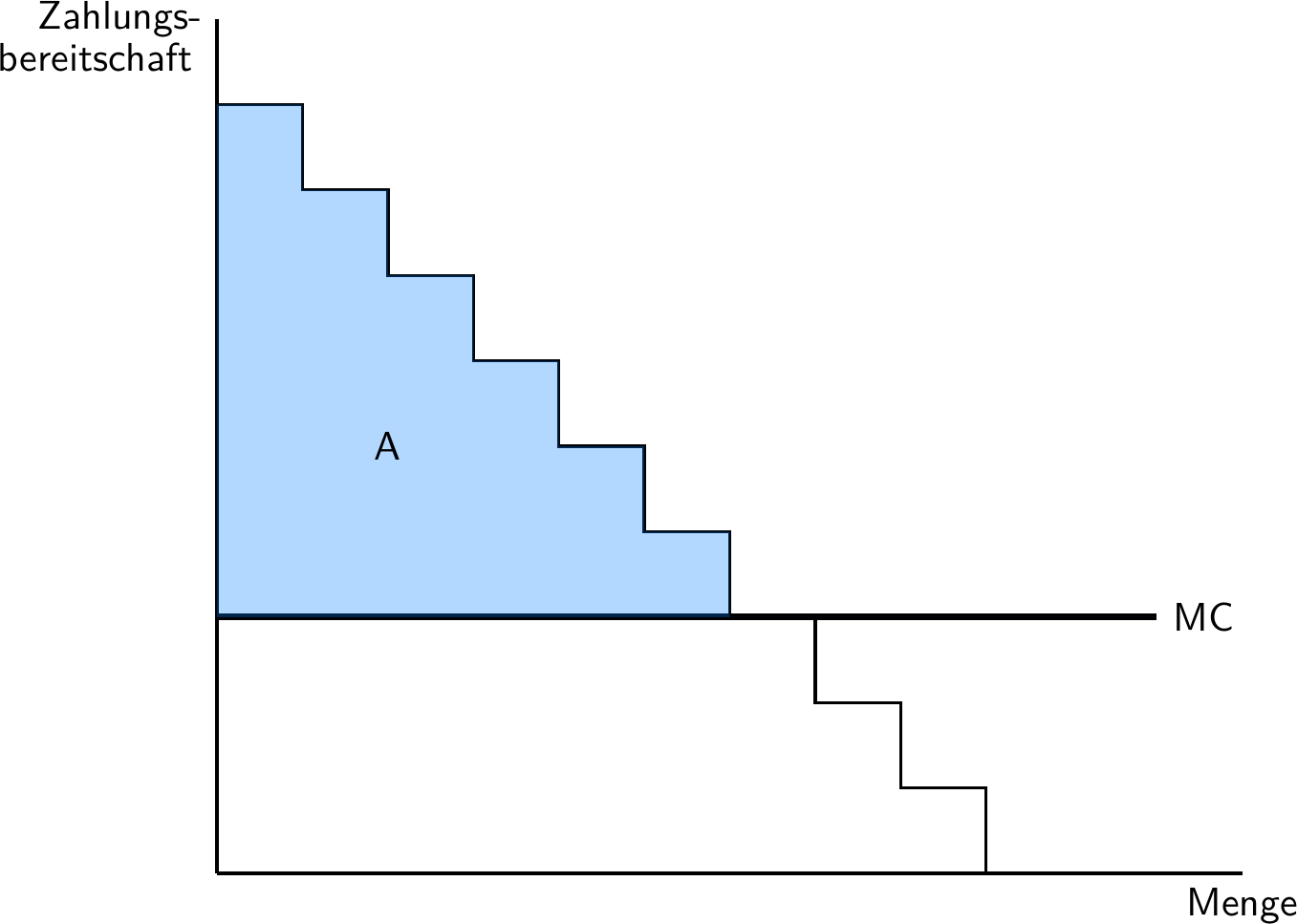
Wohlfahrt unter perfekter Preisdiskriminierung

Der Monopolist eignet sich die gesamte Konsumentenrente an

Somit ist diese Situation Pareto-effizient

Der Monopolist hat Anreize, jede:n Konsument:in mit einer Zahlungsbereitschaft oberhalb der Grenzkosten zu bedienen
Die verkaufte Menge ist also genau so hoch wie im vollständigen Wettbewerb
Aus Verteilungsgesichtspunkten gibt es natürlich Fragezeichen

Preisdiskrimierung Dritten Grades

Oft wissen Unternehmen zwar nicht alles über ihre Kund:innen, aber zumindest ein bisschen

Bestimmte Charakteristiken sind beobachtbar, wie z.B. das Alter, das Geschlecht, ein Status, der Wohnort
Wenn diese mit Zahlungsbereitschaft korrelieren, kann ein Unternehmen preisdiskriminieren

Dies wird auch als Segmentierung bezeichnet; Es gibt also Gruppenpreise

Ebenfalls ein Fall von direkter Preisdiskriminierung, da Kundentypen vor dem Kauf getrennt werden
Gruppen mit unelastischer Nachfrage müssen höhere Preise zahlen

Beispiel: Studentenpreise im Kino

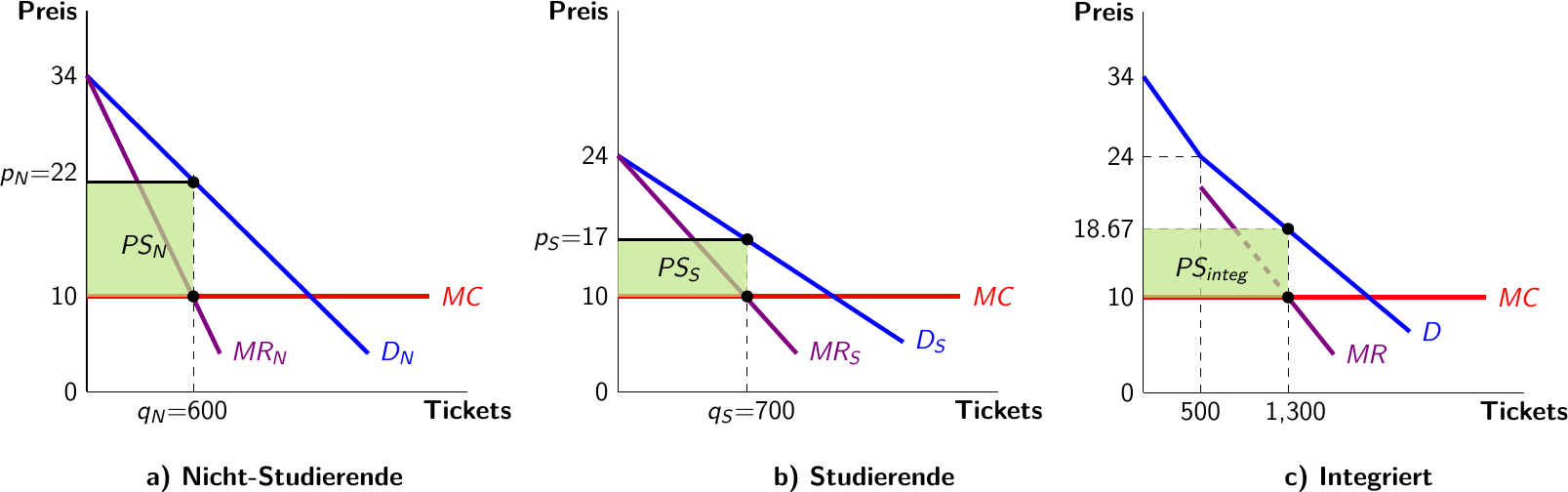
Produzentenrente

Integration: \(PS_{integ}=(18.67-10)*1.300 = 11.271\)
Segmentierung: \(PS_{N}+PS_{S}=12*600+7*700 = 12.100 \ (>PS_{integ})\)

Konsumentenrente

Integration: \(CS_{integ}=0.5*10*500 + 5.33*500 + 0.5*5.33*800=7.297\)
Segmentierung: \(CS_{NS}+CS_{S}=0.5*12*600+0.5*7*700=6050 \ (<CS_{integ})\)
In diesem Fall können die zusätzlichen Studierendenrenten die Verluste der anderen nicht kompensieren

Preisdiskriminierung Zweiten Grades

Oft können Unternehmen ihre Konsument:innen erst nach Zahlungsbereitschaft (ihrem “Typ”) trennen, nachdem das Kaufverhalten beobachtet wurde

Unternehmen bieten Preis-Menge Kombinationen an; Konsument:innen selektieren sich selbst
Wird auch nicht-lineare Preissetzung genannt und ist ein Fall von indirekter Preisdiskriminierung

Solche “Menüs” sind weit verbreitet

Business vs economy class (caveat: hier gibt es auch vertikale Produktdifferenzierung)
Mengenrabatte (“block pricing”)

“Smart Menus”

Die Herausforderung bei Menüs ist, dass Konsument:innen auch die für sie vorgesehene Option wählen wollen, a.k.a. Anreizkompatibilität

Wenn business class zu teuer ist, werden auch Geschäftsreisende auf economy umsteigen
Wenn der Preisunterschied zwischen business und economy zu klein sind, fliegen Urlauber business
Der Marktsegmentierung sind also klare Grenzen gesetzt

Wer höhere Preise zahlt und wer mehr von seinen Renten behalten darf, hängt von der relativen Nachfrageelastizität ab

Geschäftsreisende haben eine niedrigere Elastizität (Zeitdruck, Erfolgsdruck etc.) und zahlen typischerweise höhere Preise

Weitere verwandte Preisstrategien: Bundling

Bundling

Mindestens zwei Produkte werden nur als Bündel verkauft, wobei die Einzelprodukte negativ korrelierte Zahlungsbereitschaften über Kundengruppen hinweg haben
Beispiele: MS Office Suite, Fernsehpakete wie Sky/Disney plus/Netflix

Beispiel: TV Pakete

Maximale Preise betragen 9 und 1 EUR für die einzelnen subscriptions; Umsatz ist 20 EUR
Das Bündel zu 10,50 EUR erzielt einen Umsatz von 21 EUR

	Bundesliga	Seifenopern	Bündel
Anna	9 EUR	1,50 EUR	10.50 EUR
Zoe	10 EUR	1,00 EUR	11,00 EUR

Weitere verwandte Preisstrategien: Zweigeteilte Preise

Viele Güter und Dienstleistungen haben eine fixe und eine variable Komponente

Eintritt und Fahrten in Vergnügungsparks
Spielekonsolen und Spiele, Telefonverträge
Rasierer und Klingen, Drucker und Patronen etc.

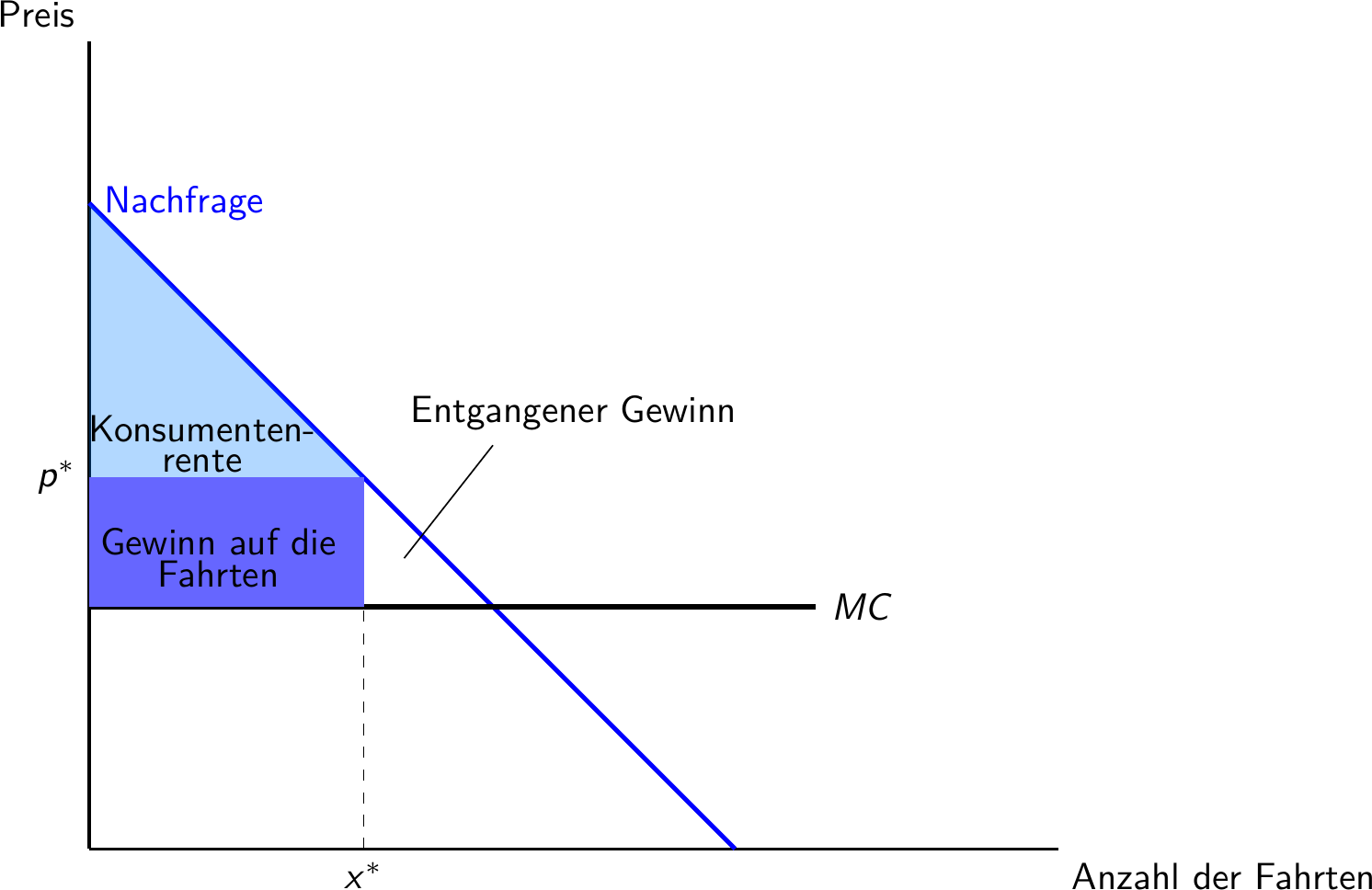
Nehmen wir an, alle Besucher:innen von Disneyland sind identisch und haben eine fallende Nachfrage

Je günstiger die Fahrten, desto höher die Nachfrage

Außerdem nehmen wir konstante Grenzkosten an

Teamarbeit: Welche Preisstrategie sollte Disneyland verfolgen?

Zweigeteilte Preise in Vergnügungsparks

Produktdifferenzierung

Motivation

Ein häufiger Grund für Marktmacht ist Produktdifferenzierung: Unternehmen kreieren Varianten von Gütern, die sich voneinander unterscheiden

Definitionen und Auswirkungen

Wir unterscheiden zwei Arten (caveat: Definitionen sind grob)

Horizontale Produktdifferenzierung: Zum gleichen Preis kaufen unterschiedliche Kund:innen unterschiedliche Varianten (z.B. Autos innerhalb einer Klasse)
Vertikale Produktdifferenzierung: Zum gleichen Preis kaufen unterschiedliche Kund:innen die gleiche Variante (z.B. Autos über Klassen hinweg)

Auswirkungen

Je stärker die Differenzierung, desto weniger gut können Konsument:innen substituieren und desto unelastischer die Nachfrage
Gleichzeitig verliert man Kund:innen an die Konkurrenz
Der optimale Grad der Differenzierung wird optimal gewählt und hängt von der Stärke der beiden Effekte ab

Bertrand Wettbewerb mit Differenzierung: Die Eisverkäufer

Zwei Eisverkäufer:innen bieten das gleiche Sortiment und positionieren sich an verschiedenen Stellen eines Strandes

Der Strand erstreckt sich über das Interval \([0,1]\) und eine Masse \(1\) von Besuchern hat sich etwa gleichverteilt niedergelassen
Jede:r Besucher:in erhält den gleichen Nutzen \(u\) von einem Eis und kann bzw. will sich nicht mehr leisten (diskrete Wahl)
Jede:r Konsument:in wählt immer den nächstgelegenen Eisverkäufer
Der Preis ist durch das Eiskartell festgelegt

Teamarbeit: Wo werden sich die Eisverkäufer:innen optimalerweise positionieren?

Hotellings Gesetz

Nehmen wir an, dass sie sich an unterschiedlichen Orten aufstellen, der erste etwas weiter links (L), der zweite etwas weiter rechts (R)

L hat eine einseitig profitable Abweichung: Etwas weiter rechts kann L ein paar Kunden von R anlocken, verliert aber niemanden auf der linken Seite (Gleiches gilt für R)
Das einzige Nash Gleichgewicht ist, dass sich beide in der Mitte positionieren und den Markt hälftig aufteilen

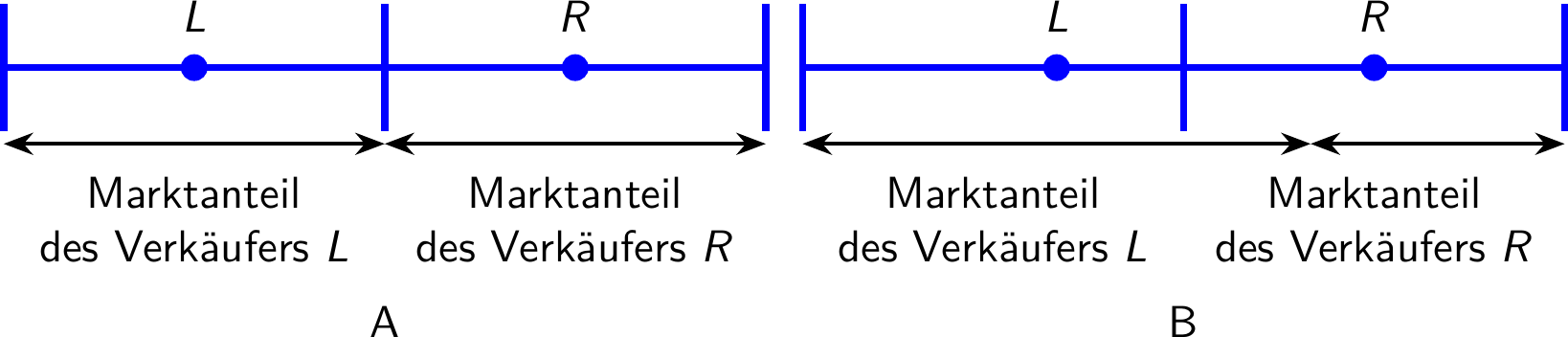
Implikationen

Das Gleichgewicht ist nicht Pareto-optimal: die Wegkosten wären bei \(s_L = 0.25\) und \(s_R = 0.75\) minimiert
Produzenten streben minimale Differenzierung an, obwohl Kund:innen das so nicht wünschen
Kann auch auf Politik übertragen werden (Medianwähler-Theorem)

Auflösung des Bertrand Paradox

Nehmen wir nun an, dass die Eisverkäufer ihre Preise selbst setzen können, keine Grenzkosten haben und Konsument:innen immmer ihren Nutzen minus Wegkosten und Preis maximieren

Im Gleichgewicht \(s_L=s_R=0.5\) zählt für jede:n Konsument:in nur der Preis, sodass die Residualnachfragen vollständig elastisch sind
Bewegt sich L z.B. ein wenig nach links, kann L den Preis u.U. etwas erhöhen
- Konsument:innen links von L werden weiter von L kaufen, sodass der Umsatz steigt
- Allerdings verliert L an Kund:innen zwischen R und L
Ob eine Abweichung, also eine Produktdifferenzierung für L und R optimal ist, hängt von den Wegkosten und der Verteilung der Urlauber:innen ab

Erkenntnis: Produktdifferenzierung kann Wettbewerb abschwächen und das Bertrand Paradox auflösen

Monopolistischer Wettbewerb

In Industrien mit a) horizontaler Produktdifferenzierung und b) niedrigen Marktzugangsbarrieren kommt es zu einer besonderen Markstruktur

Jedes Unternehmen verhält sich wie ein Monopolist für seine eigene Variante (fallende Residualnachfrage + Preis-/Mengensetzung)
Durch Marktein- und -austritt werden positive Gewinne auf Null reduziert

Diese Marktstruktur heißt Monopolistischer Wettbewerb

Beispiele

Restaurants in der Innenstadt
Friseure, Hotels, Buden am Weihnachtsmarkt

Funktionsweise des Monopolistischen Wettbewerbs

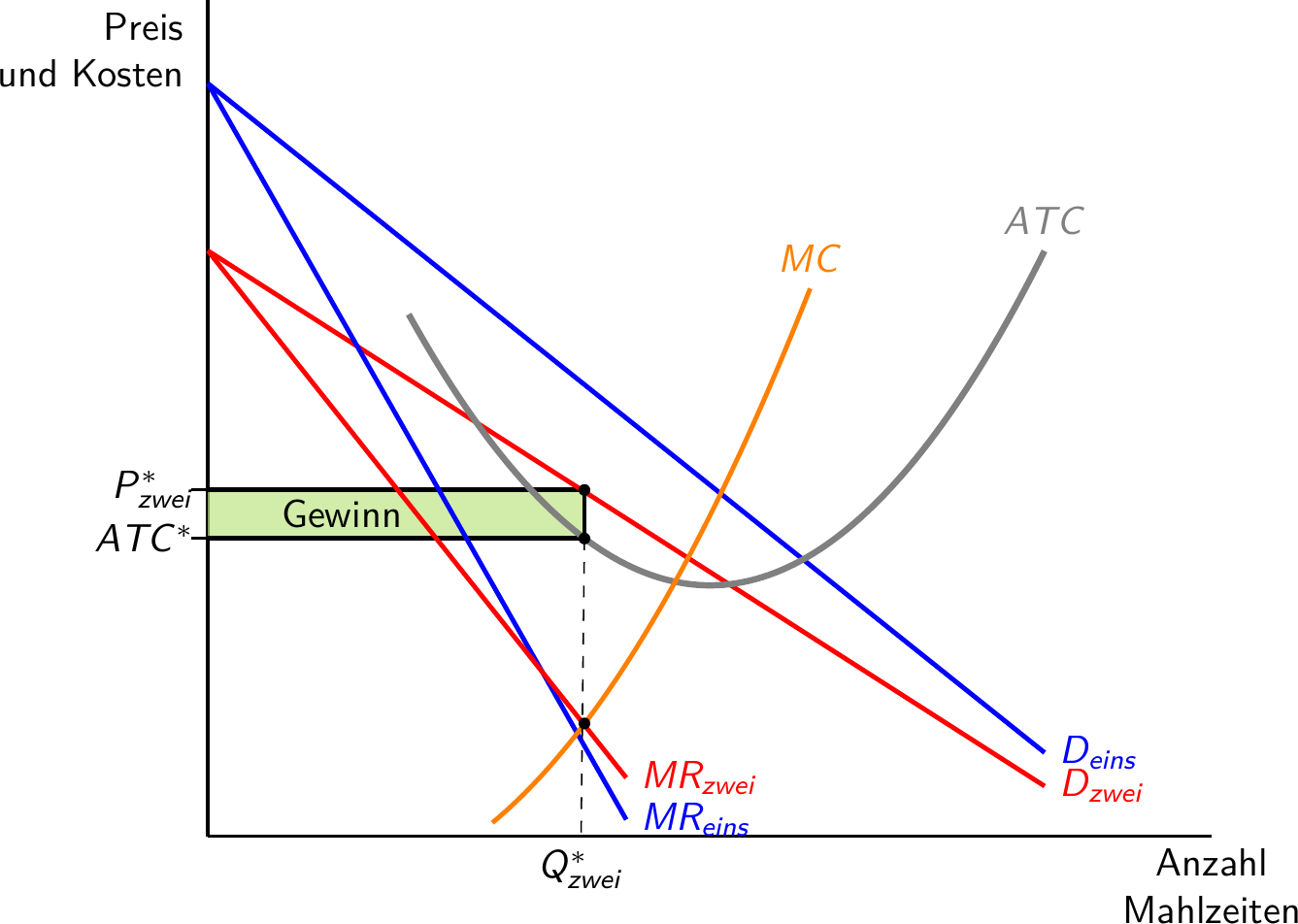
Wohlfahrtsimplikationen

Eine Wohlfahrtsbetrachtung des monopolistischen Wettbewerbs ergibt interessante Besonderheiten

Da der Preis die Grenzkosten übersteigt, liegt kein Pareto-Gleichgewicht vor
Unternehmen produzieren unterhalb ihrer effizienten Betriebsgröße, sodass weniger Marktteilnehmer die Effizienz erhöhen könnten (“Überkapazitäten”)
Die Zahl der Produktvarianten stiftet Nutzen, da Konsument:innen mit unterschiedlichen Präferenzen ein passenderes Produkt finden können

Wiederholungsfragen I

Vollziehen Sie die Rechnungen auf den Folien 8 bis 11 nach. Berechenen Sie die Konsumentenrente, die Produzentenrente und den Wohlfahrtsverlust, und verifizieren Sie Ihre Ergebnisse mithilfe der App auf Folie 12. Erklären Sie in eigenen Worten, warum das Gleichgewicht auf einem Monopolmarkt nicht Pareto-effizient ist.
Fassen Sie die Besonderheiten eines natürlichen Monopols in Ihren Worten zusammen.
Beschreiben Sie, inwiefern sich die substanziellen Annahmen der drei Oligopol-Modelle unterscheiden.
Erklären Sie die Unterschiede der jeweiligen Gleichgewichte im Bertrand und im Cournot Wettbewerb mit eigenen Worten.
Erklären Sie, warum und unter welchen Umständen Kartelle für Unternehmen interessant sind. Was sollten Wettbewerbsbehörden tun?

Wiederholungsfragen II

Erklären Sie die Unterschiede zwischen den drei Varianten der Preisdiskriminierung.
Betrachten Sie drei Industrien, die Sie gut kennen. Welche der von uns behandelten Preisstrategien können Sie dort finden? Welche Voraussetzungen sind jeweils erfüllt? Welche Wohlfahrtsimplikationen gibt es?
Erklären Sie, was Produktdifferenzierung ist, warum Unternehmen diese praktizieren, und welche Gleichgewichts- und Wohlfahrtimplikationen sie hat.

Notes and feedback

Es wäre gut, noch einen slide zu haben der explizit sagt, dass man als Monopolist sowohl Menge als auch Preis setzen kann
lecture 1: slide 20; perhaps a little too slow. Did the evaluation (first part)
lecture 2: slide 39; didn’t finish cartel stability within (digression), looks like it was a bit too much or I was too slow. Did the second part of the evaluation. Not sure what difference it made. –> maybe more interaction? But it’s difficult
lecture 3: finished, but omitted nearly all of bundling and two-part tariffs (just explained them very briefly in intuition) and just mentioned monopolistic competition in the last 5 minutes or so. There was very little interaction and the lecture was missing structure. Maybe break it up.
slide 41: Einen Überblick einbauen, was wir in dem Kapitel alles machen
slide 47: Mengenrabatte sind nicht das gleiche wie block pricing - letzteres ist abschnittsweise, wohingegen sich Mengenrabatte auf alles beziehen. Außerdem gehören die anderen Strategien wie bundling auch dazu und sollten hier im Überblick aufgeführt werden
slide 54: “optimal” doppelt am Ende
slide 58: anderes Beispiel als economy vs business, denn das Beispiel ist etwas irreführend
slide 55: Hotelling, nicht Bertrand; hier habenw ir ein Eisverkäufer Kartell

MikroökonomieVorlesung 5

Einführung

Motivation: Marktversagen

Motivation: Marktmacht

Überblick und Resourcen

Monopolverhalten und Wohlfahrt

Entstehung von Monopolen

Das Gewinnmaximierungsproblem

Optimalitätsbedingung

Beispiel: Lineare Nachfrage

Monopolgleichgewicht mit linearer Nachfrage

Diagramm: Monopolverhalten bei linearer Nachfrage

Komparative Statik im Monopol

Preissetzung im vollständigen Wettbewerb

Preissetzung im Monopol

Ineffizienz des Monopols

Diagramm: Wohlfahrt im Monopol bei linearer Nachfrage

Wohlfahrt im Vergleich zum Benchmark

Spezialfall: Natürliches Monopol

Grafik Natürliches Monopol

Oligopole

Übersicht

Anwendung: Preiswettbewerb für Chips

Das Bertrand Duopol

Das Bertrand Paradox

Auflösung des Bertrand Paradox

Mengenwettbewerb: Kapazitätsbeschränkungen

Das Cournot Modell

Lösung des Cournot Duopols

Vergleich: Bertrand vs Cournot

Dynamischer Wettbewerb

Das Stackelberg Modell

Lösung des Stackelberg Spiels

Stackelberg Lösung mit linearer Nachfrage

Marktführer-Vorteil

Das Vitamin-Kartell

Kartellverhalten im Duopol

Exkurs: Stabilität eines bestehenden Kartells I

Exkurs: Stabilität eines bestehenden Kartells II

Preisdiskriminierung

Motivation

Preisdiskriminierung Ersten Grades

Diagramm: Perfekte Preisdiskriminierung

Wohlfahrt unter perfekter Preisdiskriminierung

Preisdiskrimierung Dritten Grades

Beispiel: Studentenpreise im Kino

Preisdiskriminierung Zweiten Grades

“Smart Menus”

Weitere verwandte Preisstrategien: Bundling

Weitere verwandte Preisstrategien: Zweigeteilte Preise

Zweigeteilte Preise in Vergnügungsparks

Produktdifferenzierung

Motivation

Definitionen und Auswirkungen

Bertrand Wettbewerb mit Differenzierung: Die Eisverkäufer

Hotellings Gesetz

Auflösung des Bertrand Paradox

Monopolistischer Wettbewerb

Funktionsweise des Monopolistischen Wettbewerbs

Wohlfahrtsimplikationen

Wiederholungsfragen I

Wiederholungsfragen II

Mikroökonomie
Vorlesung 5