Mikroökonomie
Vorlesung 4: Spieltheorie
Prof. Frank Pisch PhD
Einführung
Motivation: Strategische Preis- und Werbeinteraktion

Bekriegen sich seit etwa 130 Jahren mit Preissenkungen, z.B. während des Superbowls
- Eine Preissenkung des einen führt typischerweise zu Preissenkungen durch den anderen
Ähnlich robust geht es im Werbemarkt zu, wo beide extrem aktiv und kreativ agieren (“Cola-Wars” in den 1970ern und 80ern)
Motivation: Strategische Mengeninteraktion

Wettberb mit Investitionen in Produktionskapazität sowie Teile und andere Inputs
- Höhere Mengen des einen Unternehmens führen zu Reduktionen beim anderen, um Preise zu stabilisieren (der Markt ist überschaubar)
Design- und Modellentscheidungen werden hochstrategisch getroffen
Motivation: Weitere Anwendungsbereiche der Spieltheorie
Wirtschaftswissenschaften:
Auktionen, z.B. von Rechten zur Nutzung von Bandbreiten für Mobiltelefonie, Organspende, CO2 Lizenzen, öffentliche Beschaffung
Ökonomische Beziehungen wie Arbeitgeber-/Arbeitnehmer-Verhältnisse oder bilaterale Kaufentscheidungen sind von strategischen Motiven bestimmt (z.B. Informationsasymmetrien und Vertragsunvollständigkeit, Karrieremotive)
Politikwissenschaften:
Politischer Wettbewerb zwischen Parteien und Kandidat:innen
Internationale Konflikte, z.B. ökonomischer oder militärischer Natur
Biologie und Ökologie:
- Evolutionstheorie, insbesondere stabile Strategien wie Aggression, Kooperation, Altruismus
Computerspiele, Physik, Informatik, etc. pp.
Überblick und Ressourcen
Ziele
Die weitverbreitete Sprache der Spieltheorie erlernen und benutzen
Gleichgewichtskonzepte verstehen und benutzen
Strategische Interaktionen modellieren
Ressourcen
Kapitel im Varian: 29, 30
YouTube, ChatGPT, Spiele-App am Ende
Definitionen, Konzepte und ein erstes Beispiel
Beispiel: Gefangenendilemma
Das vielleicht bekannteste Spiel ist das Gefangenendilemma
Zwei Täter verüben einen Banküberfall, können aber gefasst werden
Sie werden in zwei unterschiedliche Zellen gesperrt und können nicht kommunizieren
Es gibt zu wenige Hinweise und man ist auf die Aussagen der beiden angewiesen
Gestehen beide, erhalten sie jeweils 2 Jahre Gefängnis
Gesteht jeweils nur einer während der andere schweigt, wird der Geständige aufgrund der Kronzeugenregelung freigelassen, der Verweigerer bekommt 3 Jahre Gefängnis
Schweigen beide, bekommen beide ein Jahr
Auszahlungsmatrix im GD
Wir können das Spiel leicht mithilfe einer Auszahlungsmatrix darstellen
| Spieler:in 2 | |||
|---|---|---|---|
| Schweigen | Reden | ||
| Spieler:in 1 | Schweigen | (-1, -1) | (-3, 0) |
| Reden | ( 0, -3) | (-2, -2) | |
Der erste Eintrag in jeder Zelle ist der payoff für Spieler:in 1, der zweite für Spieler:in 2
Die Strategien sind einfach, da jeweils nur eine Entscheidung getroffen werden muss und man das Verhalten des anderen nicht kennt
Teamarbeit: Wie geht dieses Spiel aus?
Einige Definitionen
Die Spieltheorie lässt sich grob in kooperative und non-kooperative Spieltheorie gliedern
- Wir beschäftigen uns mit Situationen, in denen Spieler:innen nicht kooperieren
Spieler:innen
- Grundsätzlich mindestens 2 Entscheider, aber \(n\geq2\)
Strategien
Pläne, an welchem Punkt bzw. unter welchen Bedingungen welche Entscheidung getroffen wird
Sie betreffen immer das gesamte Spiel, also alle Entscheidungen
Wir unterscheiden
reineStrategien, die deterministisch sind, undgemischteStrategien, in denen wir würfeln
Payoffs oder Auszahlungen
Dies sind die “Resultate”: Wieviel erhält jeder Spieler und unter welchen Bedingungen
Spiele können oft mithilfe einer
Auszahlungsmatrixcharakterisiert werden
Optimale Strategien und ein Gleichgewicht in dominanten Strategien
Wie geht das Gefangenendilemma aus?
Wir benutzen wiederum das Konzept eines Gleichgewichts
Also eine Situation, in der keine der Parteien einen Anreiz hat, von ihrer Strategie abzuweichen
Das Ergebnis ist somit in gewisser Weise
stabil, was für empirische Arbeit extrem wichtig ist
Im Fall des GD ist es leicht: Beide Spieler:innen haben eine strikt dominante Strategie, nämlich “Reden”
Strikt dominant bedeutet, dass diese Strategie immer strikt bessere payoffs verspricht als andere Strategien
Schwachdominantheißt, dass diese Strategie nie schlechter ist als alle anderen StrategienWir haben also ein
GleichgewichtinstriktdominantenStrategien
Beispiel: Gleichgewicht im GD
| Spieler:in 2 | |||
|---|---|---|---|
| Schweigen | Reden | ||
| Spieler:in 1 | Schweigen | (-1, -1) | (-3, 0) |
| Reden | ( 0, -3) | (-2, -2) | |
(Reden,Reden) ist ein Gleichgewicht, da sich beide nur schlechter stellen können
Einsicht des GD: individuell rationales Verhalten führt hier zu einem sozial unglücklichen Ergebnis!
- Handelskriege, Rüstungskontrolle, bestimmte Konflikte
Zumeist hängt die optimale Strategie jedoch vom Verhalten des:r anderen ab…
Das Nash-Gleichgewicht
John Nash
Die vielleicht wichtigste Gleichgewichtsidee stammt von einem Mathematiker, John Nash (*1928–†2015)
Professor am MIT, später Arbeit in Princeton
Nobel Preis 1994 für seine Beiträge zur Spieltheorie (mit John Harsanyi und Reinhard Selten)
- Bedeutende Beiträge auch zur Mathematik und Kryptographie
Litt unter schwerer Schizophrenie; bekannt durch den Oscar-prämierten Film “A Beautiful Mind”

Eine intuitive Gleichgewichtsidee
Gleichgewichte in dominanten Strategien treten sehr selten auf
Wir beobachten trotzdem, dass sich in Spielen stabiles Verhalten einstellt
Ein anderes Gleichgewichtskonzept muss her!
Nash’s Idee war so einfach wie bedeutsam:
- Eine Kombination von Strategien stellt ein
Nash-Gleichgewichtdar, wenn jede:r Spieler:in die optimale Strategie spielt, gegeben die Strategien der/des anderen
Mit anderen Worten, jeder spielt die beste Antwort auf die Gleichgewichtsstrategien der anderen
Erwartungenüber das Verhalten der anderen Spieler:innen stimmen mit deren Handlungen überein
Beispiel: Das Koordinationsspiel (Battle-of-the-Sexes)
| Spieler:in 2 | |||
|---|---|---|---|
| Oper | Fußball | ||
| Spieler:in 1 | Oper | (2, 1) | (0, 0) |
| Fußball | ( 0, 0) | (1, 2) | |
Zwei Spieler:innen, die sich nicht koordinieren können, haben die Wahl, wo sie hingehen
- Sie haben eigene Präferenzen, finden es aber schön, zusammen zu sein
Teamarbeit: Wie geht das Spiel im Sinne von Nash aus?
Beispiel: Das Koordinationsspiel (Battle-of-the-Sexes)
| Spieler:in 2 | |||
|---|---|---|---|
| Oper | Fußball | ||
| Spieler:in 1 | Oper | (2, 1) | (0, 0) |
| Fußball | ( 0, 0) | (1, 2) | |
Es gibt hier zwei Nash-Gleichgewichte: (O,O) und (F,F)
Bei (O,O) wird Spieler:in 1 nicht
einseitigabweichenwollen, da Fußball allein keinen Spaß machtGleiches gilt für Spieler:in 2, auch wenn sie Fußball vorziehen würde
Das gleiche Argument hält für (F,F)
Beachte: Es gibt noch ein weiteres Nash-Gleichgewicht, nämlich in gemischten Strategien – dazu später mehr!
Beispiel: Das Hawk-Dove Game (Chicken Game)
| Spieler:in 2 | |||
|---|---|---|---|
| Hawk | Dove | ||
| Spieler:in 1 | Hawk | \(\left (\frac{V}{2}-C, \frac{V}{2}-C \right)\) | \((V, 0)\) |
| Dove | \((0, V)\) | \(\left (\frac{V}{2}, \frac{V}{2} \right)\) | |
Diese Situation verkörpert den Kampf um eine Ressource \(V\) (oder eine Mutprobe)
Zeigen beide aggressives oder beide zurückweichendes Verhalten, wir die Resource hälftig aufgeteilt
Kämpfen verursacht jedoch Kosten \(C\)
\(V/2-C\) kann positiv oder negativ sein
Zeigt nur ein:e Spieler:in aggressives Verhalten, gewinnt er/sie die Resource
Teamarbeit: Finden Sie alle Nash-Gleichgewichte in reinen Strategien
Beispiel: Matching Pennies
| Spieler:in 2 | |||
|---|---|---|---|
| Kopf | Zahl | ||
| Spieler:in 1 | Kopf | (1, -1) | (-1, 1) |
| Zahl | (-1, 1) | (1, -1) | |
Wenn beide Spieler:innen die gleiche Seite wählen, gewinnt Spieler:in 1, wenn sie unterschiedliche wählen, Spieler:in 2
Teamarbeit: Finden Sie ein Nash-Gleichgewicht
Nash-Gleichgewichte in gemischten Strategien
In matching pennies gibt es nur ein Nash-Gleichgewicht: Beide Spieler:innen werfen tatsächlich eine faire Münze
Beide spielen also Kopf und Zahl mit jeweils 50% Wahrscheinlichkeit
Kein:e Spieler:in hat einen Anreiz, einseitig abzuweichen, da man sich nicht besser als \(0\) stellen kann
Um dies mathematisch zu zeigen, muss man verstehen, dass Spieler:innen, die gemischte Strategien spielen wollen, immer indifferent zwischen den reinen Strategien sein müssen
Ansonsten würden sie ja eine der Optionen strikt bevorzugen
Jede:r Spieler:in muss also die anderen mit der Strategie indifferent halten
Dies ist im Gleichgewicht offensichtlich der Fall
Nash-Gleichgewicht in Matching Pennies
Im Fall von matching pennies muss der Erwartungswert von Kopf gleich dem Erwartungswert von Zahl sein
- Gegeben die Gleichgewichtsstrategie \(Pr(s_2=\text{Kopf})=p_2^{NE}\) von Spieler:in 2 erhält Spieler:in 1 für Kopf
\[ \underbrace{p_2^{NE} * 1}_{\text{Übereinstimmung}} + \underbrace{(1-p_2^{NE}) * (-1)}_{\text{Unterschied}} = 2p_2^{NE}-1 \]
- und für Zahl
\[ \underbrace{p_2^{NE} * (-1)}_{\text{Unterschied}} + \underbrace{(1-p_2^{NE}) * 1}_{\text{Übereinstimmung}} = 1-2p_2^{NE} \]
- sodass \(p_2^{NE}\) Spieler:in 1 nur indifferent hält wenn
\[ 2p_2^{NE}-1 = 1-2p_2^{NE} \ \ \ \Leftrightarrow \ \ \ p_2^{NE}=\frac{1}{2} \]
Dies kann analog für Spieler:in 2 gezeigt werden, sodass wir ein Nash-Gleichgewicht haben
- Einseitige Abweichungen auf andere Wahrscheinlichkeiten bringen nichts – man wird ja durch die andere Spieler:in gerade indifferent gehalten!
Sequenzielle Spiele
Motivation
Bisher haben wir angenommen, dass die Spieler:innen ihre Entscheidungen gleichzeitig treffen oder nicht wussten, wie sich die anderen entschieden haben
In vielen strategischen Situationen handeln die Akteure aber sequenziell und können auf andere reagieren
Verhandlungen
Handelskonflikte, die bspw. mit Zöllen und anderen Beschränkungen geführt werden
Investitionsentscheidungen
Viele Auktionstypen
Beispiel: Markteintritt in der Luftfahrt
In den 90er und 00er Jahren expandierte Southwest Airlines aggressiv und begann, Stück für Stück viele neue Flughäfen und Routen zu befliegen
- Delta, American Airways und andere waren mit tatsächlichem Markteintritt und Bedrohungen konfrontiert
Goolsbee und Syverson (2008, QJE) dokumentieren die Reaktionen der Marktteilnehmer
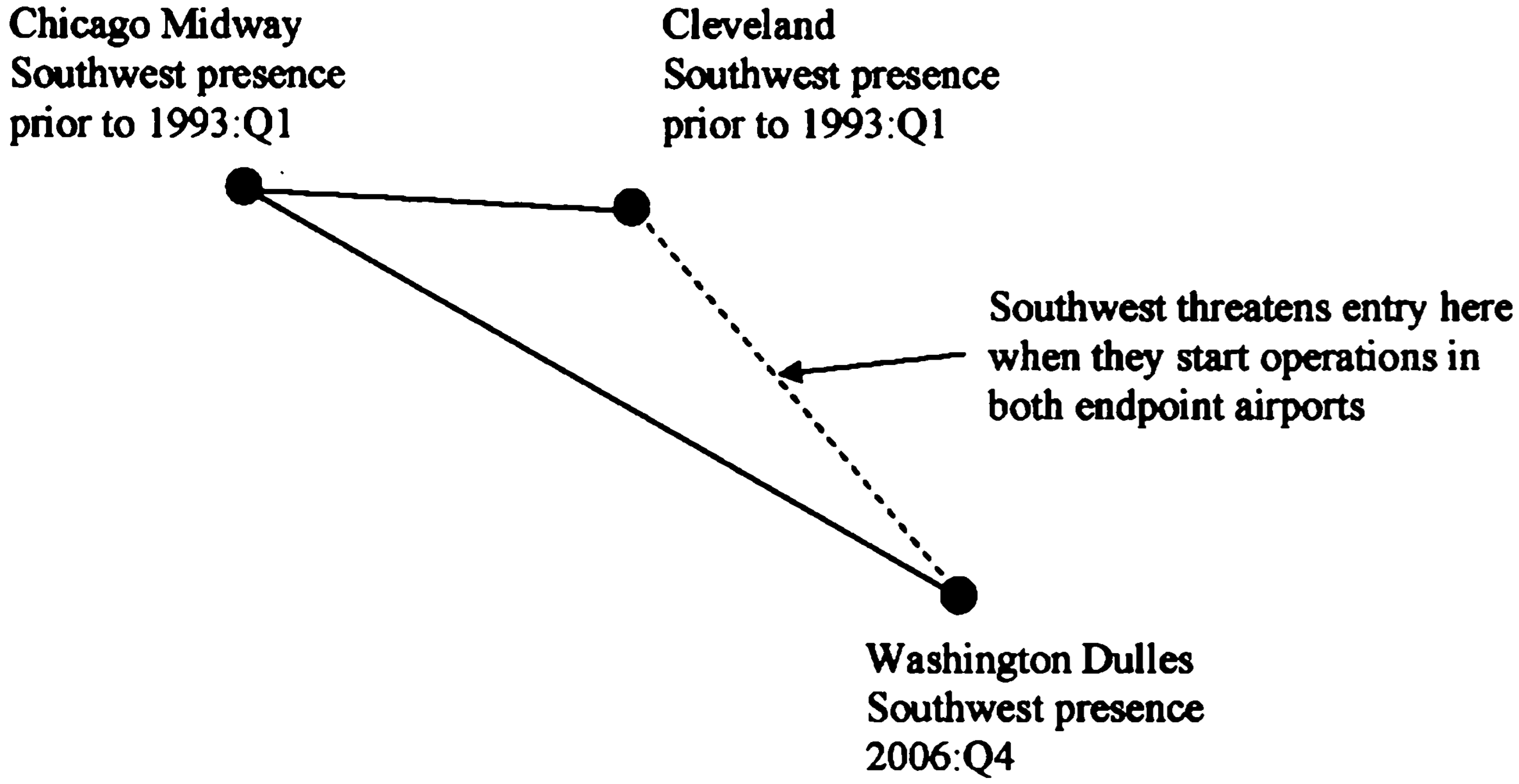
Einzigartiges natürliches Experiment: Das Routennetzwerk ermöglicht es, Bedrohungen zu identifizieren (siehe nächste Folie)
Andere Airlines kämpfen bereits vor Markteintritt: Deutlich niedrigere Preise, mehr Kapazität und mehr Reisende
Tatsächlicher Eintritt drückt Preise dann weiter
Wie können wir über diese strategische Situation nachdenken?
Bedrohungen in Goolsbee/Syverson 2008 QJE
Beispiel: Markteintritt
Es gibt ein bestehendes monopolistisches Unternehmen im Markt
Ein zweites Unternehmen überlegt, in den Markt einzutreten
Kommt es zu einem Markteintritt, kann der ehemalige Monopolist entweder “kämpfen” oder nicht (\(\neg\))
- Bspw. durch Preiskrieg, teure Werbekampagnen etc.
Teamarbeit: Wie geht das Spiel aus?
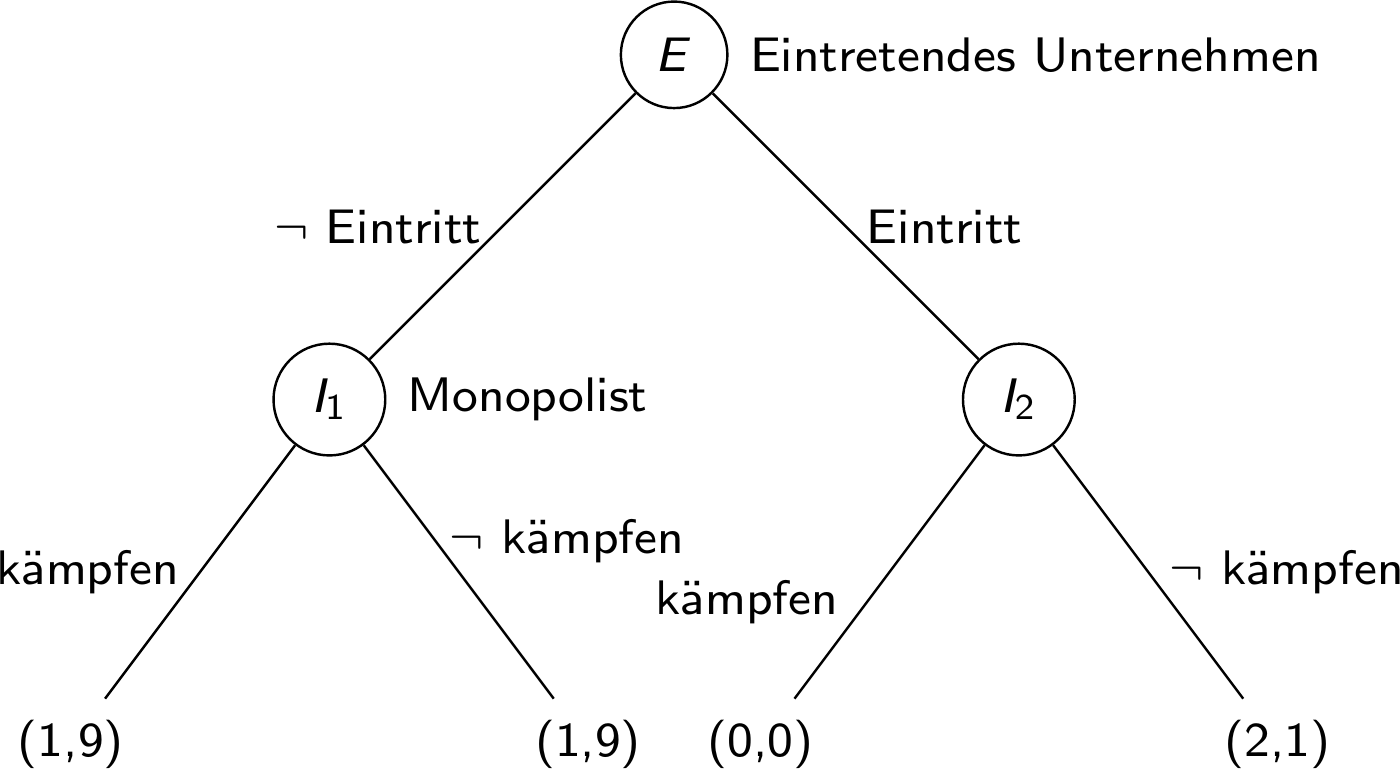
extensiver FormGleichgewichte im Markteintrittsspiel
Es gibt zwei (eigentlich drei) Nash-Gleichgewichte
- Es kommt zu “Eintritt”; der Monopolist kämpft weder nach “Eintritt” noch nach “\(\neg\) Eintritt” (oder kämpft nach “\(\neg\) Eintritt”)
- Es kommt nicht zu “Eintritt”; der Monopolist kämpft nicht nach “\(\neg\)Eintritt”, aber nach “Eintritt”
Es ist leicht zu zeigen, dass beides Gleichgewichte sind, da einseitige Abweichungen keinen Gewinn bringen
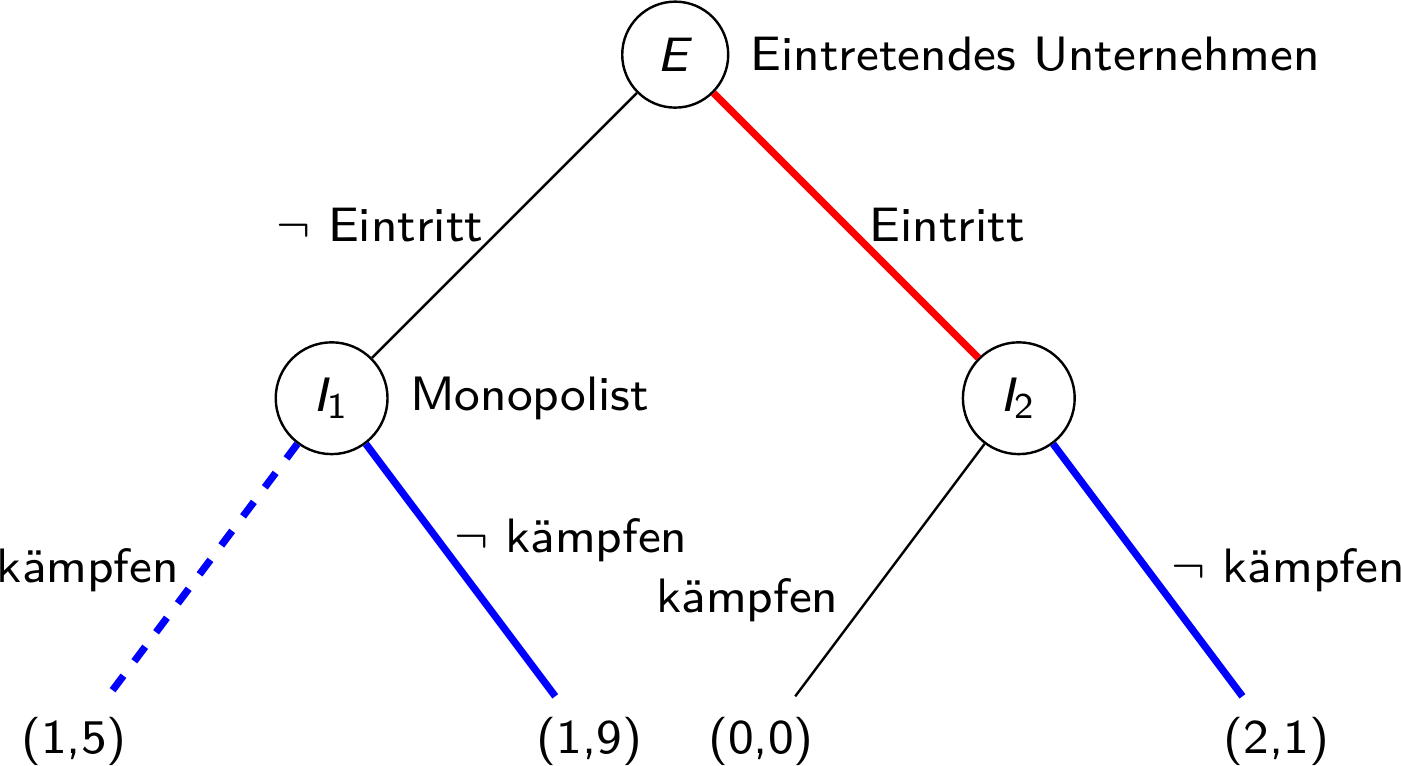
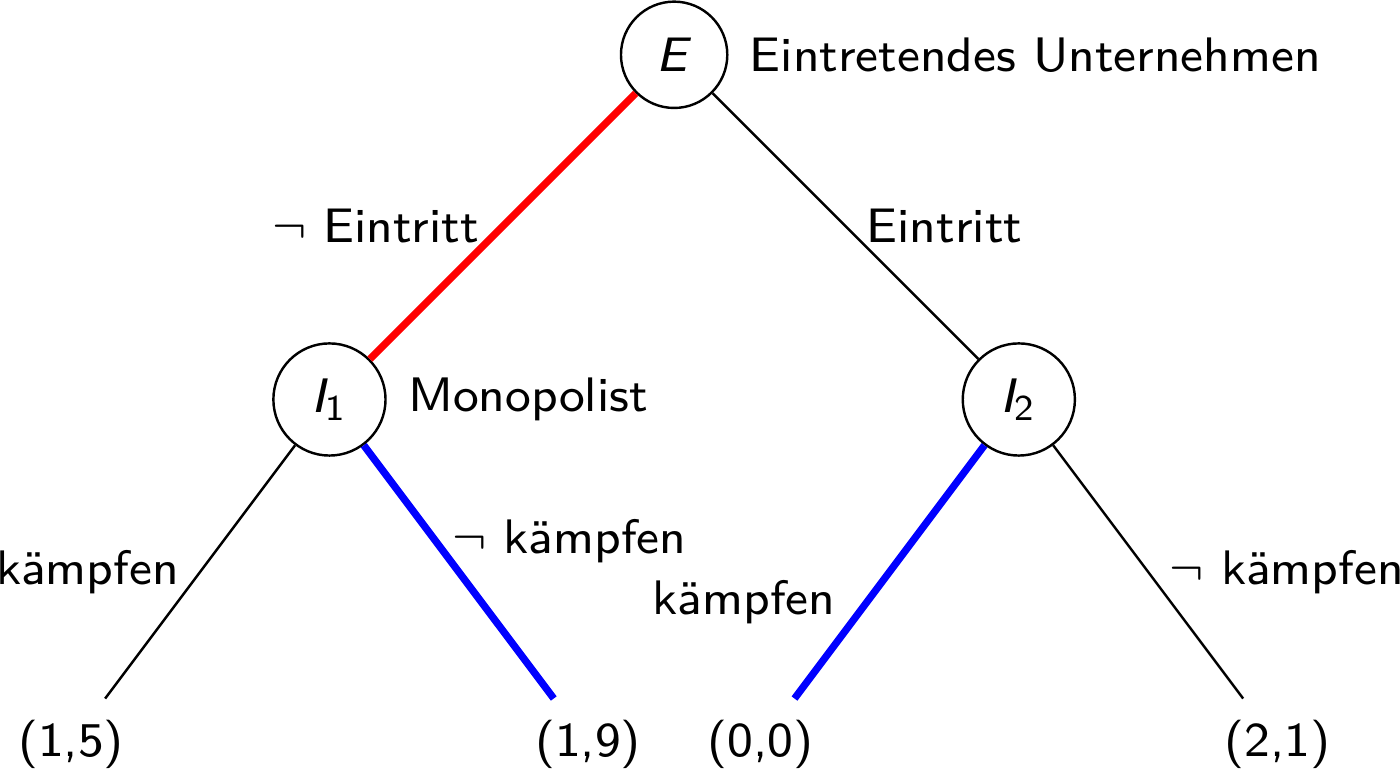
Leere Drohungen
Gleichgewicht 2 ist merkwürdig
- Für den Monopolisten wäre es völlig irrational, nach Markteintritt zu kämpfen
- Das eintretende Unternehmen sollte das vorhersehen: Der Monopolist macht eine
leereDrohung - Solch ein Gleichgewicht würde in der Realität nicht auftreten, und wir sollten einen Weg finden, es auszuschließen
Teilspielperfekte Gleichgewichte
Wir nehmen daher eine Verfeinerung unserer Gleichgewichtsidee vor
In einem
teilspielperfektenGleichgewicht induzieren die Gleichgewichtsstrategien in jedemTeilspielein Nash-GleichgewichtAnders ausgedrückt: Die Spieler:innen spielen an jedem
Entscheidungsknotenoptimale Antworten, nicht nur im ganzen Spiel
Ein Teilspiel ist das gesamte Spiel, das auf einen Entscheidungsknoten folgt
- Im Markteintrittsspiel haben wir drei Teilspiele: Eines beginnend in \(I_1\), eines beginnend in \(I_2\) und eines beginnend in \(E\) (also das gesamte Spiel)
Teilspielperfektes Gleichgewicht im Markteintrittsspiel
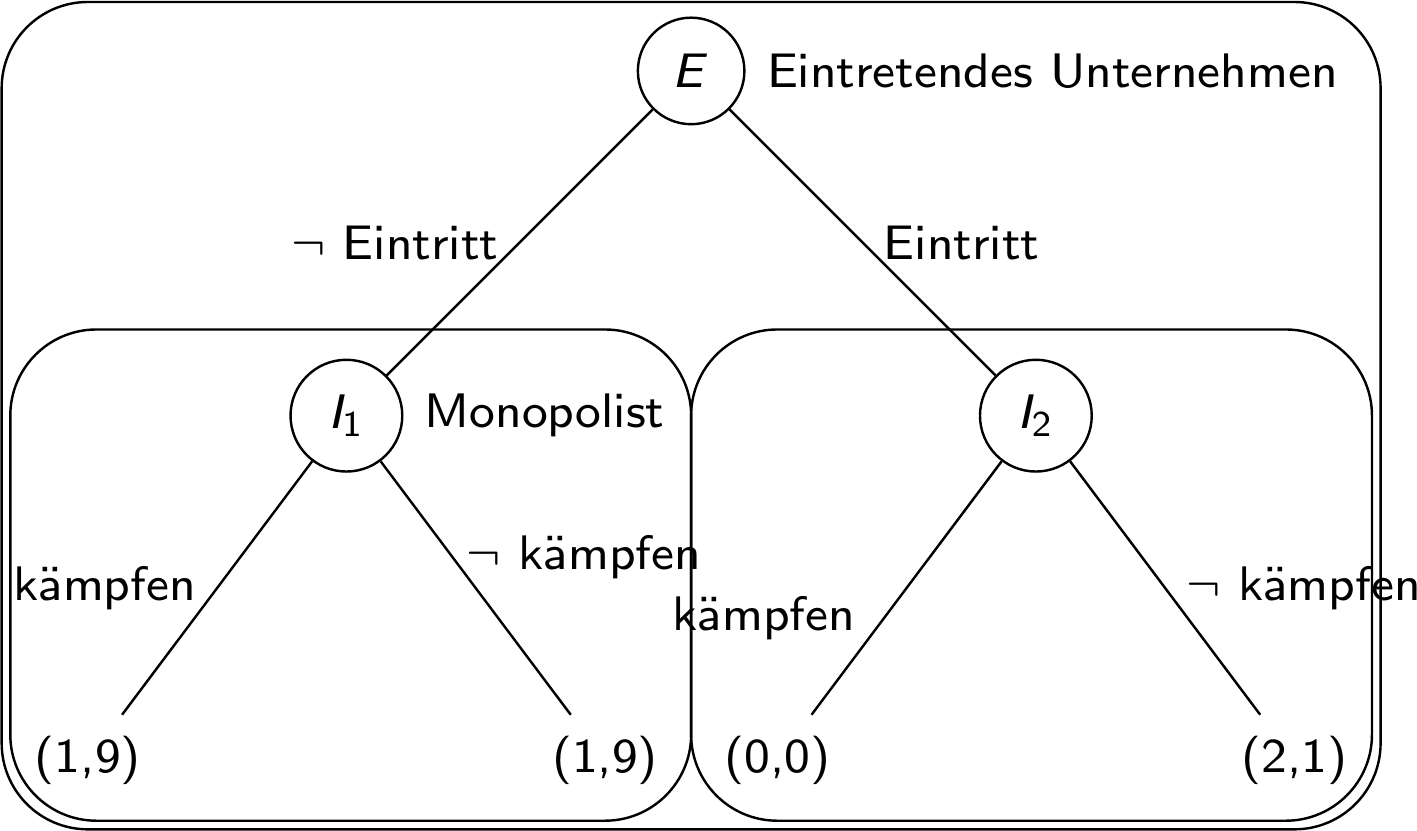
Im ersten dieser Spiele ist der Monopolist wählt er \(\neg\) kämpfen, im zweiten wählt er \(\neg\) kämpfen, und im Gesamtspiel gibt es zwei Nash-Gleichgewichte (siehe oben)
- Das Gleichgewicht mit der leeren Drohung ist somit nicht teilspielperfekt – nach Eintritt würde der Monopolist immer zurückstecken
Rückwärtsinduktion
Um teilspielperfekte Gleichgewichte zu finden, bedienen wir uns der Rückwärtsinduktion
Wir beginnen bei den letzten Teilspielen und finden das Nash-Gleichgewicht (zumeist die optimale Entscheidung)
Dann ersetzen wir die payoffs im nächstfrüheren Teilspiel und suchen wieder das Nash Gleichgewicht
Wir finden teilspielperfekte Gleichgewichte, indem wir “rückwärts”, also vom Spielende her überlegen
- Mit anderen Worten, die Spieler:innen formen rationale Erwartungen an die anderen Spieler:innen unter der Annahme, dass letztere ebenfalls rational sind
Beispiel: Entführungen
Ein Entführer hat eine Geisel genommen und überlegt, ob er sie freilassen soll
- Nach Freilassung kann sie den Entführer jedoch identifizieren
Teamarbeit: Finden Sie alle Nash-Gleichgewichte in reinen Startegien und prüfen Sie, ob sie teilspielperfekt sind
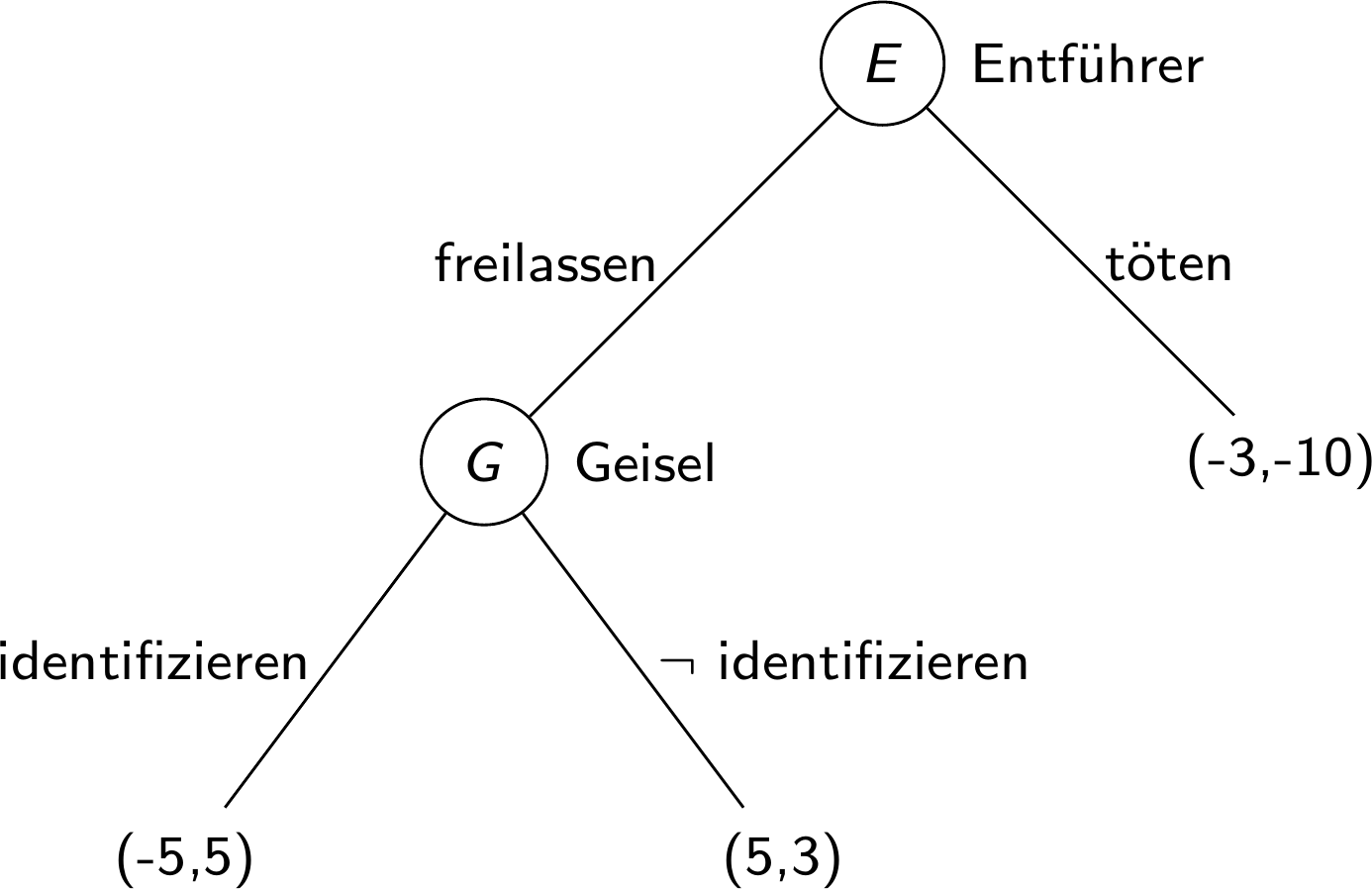
Selbstbindung
Wenn die Geisel frei ist, wird sie den Täter identifizieren wollen
- Die Tötung der Geisel ist daher Teil eines jeden teilspielperfekte Nash-Gleichgewichts
Mögliche Lösungen durch Selbstbindung
Kompromitierende Fotos der Geisel, die beim Entführer verbleiben (Schelling)
Verwandt: Drakonische Strafen für Lösegeldzahlungen (z.B. in Italien)

Wiederholte Spiele
Oft kann Kooperation auch ganz ohne Verträge oder Strafen aufrecht erhalten werden
Wenn man häufiger interagiert, bekommt man die Gelegenheit, die andere Seite zu bestrafen und so optimale Strategien zu beeinflussen
Insbesondere in
unendlich wiederholtenSpielen kann dies sehr wirksam sein (bzw. wenn das Ende zufällig/nicht vorhersehbar ist)In endlich wiederholten Spielen sind die Gleichgewichte hingegen oft degenerativ
Das unendlich wiederholte Gefangenendilemma
Nehmen wir als Beispiel das unendlich wiederholte Gefangenendilemma

In jeder Periode \(t\) wird ein GD mit den payoffs auf Folie 9 gespielt
Es gibt kein Ende des Spiels
Die Akteure gewichten die Zukunft mit dem Diskontierungsfaktor \(\delta \in (0,1)\) – je höher, desto geduldiger
- Hier: \(\delta=0.8\)
Der Raum möglicher Strategien ist sehr groß, wie in diesem Video von Veritasium bzw. Derek Muller schön erklärt
Grim Trigger Strategy
Eine mögliche Strategie ist die grim trigger strategy: Schweigen bis der andere redet; danach immer reden
Bei unkooperativem Verhalten wird die andere Person bestraft
Wenn ein:e Spieler:in also eine mögliche Abweichung betrachtet, muss sie die Bestrafung einberechnen
Ist einem die zukünftige Beziehung wichtig genug – ist man hinreichend geduldig –, wird man heute schon kooperieren
Lösung des wiederholten Gefangenendilemmas
Der payoff der grim trigger strategy im Nash Gleichgewicht ist
\[ \sum_{t=0}^{\infty} \delta^t \ \pi^{(s,s)} = \frac{\pi^{(s,s)}}{1-\delta} = \frac{-1}{1-0.8} = -5 \]
Eine potenzielle Abweichung ist, einmal zu reden (und dann nach Bestrafung weiter reden zu müssen)
\[ \pi^{(r,s)} + \sum_{t=1}^{\infty} \delta^t \ \pi^{(r,r)} = \pi^{(r,s)} + \frac{\delta \ \pi^{(r,r)}}{1-\delta} = 0 + \frac{0.8}{1-0.8}(-2) = -8 \]
In unserem Beispiel ist die Kooperation stabil
- Anwendungen: Kultur, relationale Verträge
Teamarbeit:
Was passiert, wenn \(\delta = 0.4\)?
Was passiert, wenn das Spiel nur endlich oft gespielt wird und beide Spieler dieses Ende kennen?
Ausblick
Weitere Themen in der Spieltheorie
Unvollständige Information
Oft kann man nur
Erwartungendarüber bilden, was andere tun bzw. wo man sich im Spielbaum befindetOft können Signale geschickt werden – die stimmen können, aber nicht müssen (sog. strategische Kommunikation oder cheap talk…
Oft kennt man andere Spieler:innen und ihre (oder die eigenen) Präferenzen gar nicht
Kooperative Spieltheorie
- Wie bildet man stabile Koalitionen und teilt Gewinne auf, wenn alle Akteure selbstinteressiert sind?
Mechanism Design
Beschäftigt sich mit Zuteilungsmechanismen, die bestimmte Ziele verfolgen
Beispiel: Organspendebörsen, Auktionen
Und viel mehr…
Wiederholungsfragen
Wie können Sie das Gefangenendilemma lösen?
Gehen Sie auf die nächste Folie, generieren Sie mindestens 3 payoff Matrizen, und finden Sie Gleichgewichte in strikt dominanten Strategien sowie andere Nash Gleichgewichte in reinen und gemischten Strategien – wenn sie existieren
Erklären Sie, was sequenzielle Spiele so interessant macht