Mikroökonomie
Vorlesung 2: Die Angebotsseite
Prof. Frank Pisch PhD
Einführung
Motivation: Nvidia
Die Nvidia Corporation ist einer der größten Entwickler von Grafikprozessoren und Chipsätzen für Personalcomputer, Server und Spielkonsolen
- 1993 gegründet, heute vor allem durch seine GPUs bekannt, die für KI Anwendungen notwendig sind

Motivation: Herstellung von Halbleitern
Die Herstellung und der Vertrieb von GPUs und Chipsätzen benötigt
- Silizium, Seltene Erden, sowie andere Chemikalien
- “Fabs” (Taiwan, China, USA) und hochmoderne Maschinen (von ASML)
- Forschung und Design, also Wissenschaftler und andere “high-skill” Mitarbeiter:innen + gut ausgebildete Mitarbeiter:innen im Dienstleistungsbereich (Administration, Marketing, Logistik, Catering etc.)
Aus diesem komplexen Gebilde ergeben sich wichtige Fragen
Wie sollen diese Inputs kombiniert werden, um möglichst gute Chips zu niedrigen Preisen zu produzieren?
Welche Mengen werden zu welchen Preisen angeboten, um maximale Gewinne zu erzielen?
Über Nvidia hinaus: wie sieht das Marktangebot für GPUs dementsprechend aus? Welche Wohlfahrtsimplikationen für Unternehmen ergeben sich aus Schocks?
Überblick und Ressourcen
Ziele
Modellierung des individuellen Angebots einzelner Unternehmen durch Kostenminimierung und Gewinnmaximierung
Herleitung des Branchenangebots und der Produzentenrente als Wohlfahrtskonzept
Ressourcen
Kapitel im Varian: 19, 21 - 24
Produktion und Technologie
Technologie
Ein Unternehmen benutzt Produktionsfaktoren (Inputs) um Outputs zu erzeugen
- z.B. Arbeit, Kapital, Rohstoffe, Wissen, Vor- und Zwischenprodukte werden zu Output verarbeitet

Nvidia
Eine Technologie beschreibt, welche Kombinationen von Faktoren zu welchen Outputs führen können, also welche Produktionspläne durchführbar sind
Die Produktionsfunktion
Die Produktionsfunktion beschreibt die maximal mögliche Outputmenge bei verschiedenen Inputbündeln \[
y = f(x_1,...,x_n)=f(\boldsymbol{x})
\] Die Funktionen selbst ähneln unseren Nutzenfunktionen, da ähnliche Eigenschaften wichtig sind (Cobb-Douglas, perfekte Substitute, perfekte Komplemente etc.)
Zumeist sind Produktionsfunktionen monoton
Mehr von einem Input generiert mehr Output
Das
Grenzprodukt(Marginal Product) eines Faktors ist also positiv: \(MP_i\equiv \partial y(\boldsymbol{x})/\partial x_i \geq 0\)
Meist sind sie auch konvex: “die Mischung macht’s”, denn Grenzprodukte fallen im Faktoreinsatz
\[ \partial MP_i/\partial x_i \leq 0 \]
Illustration: Grenzprodukte
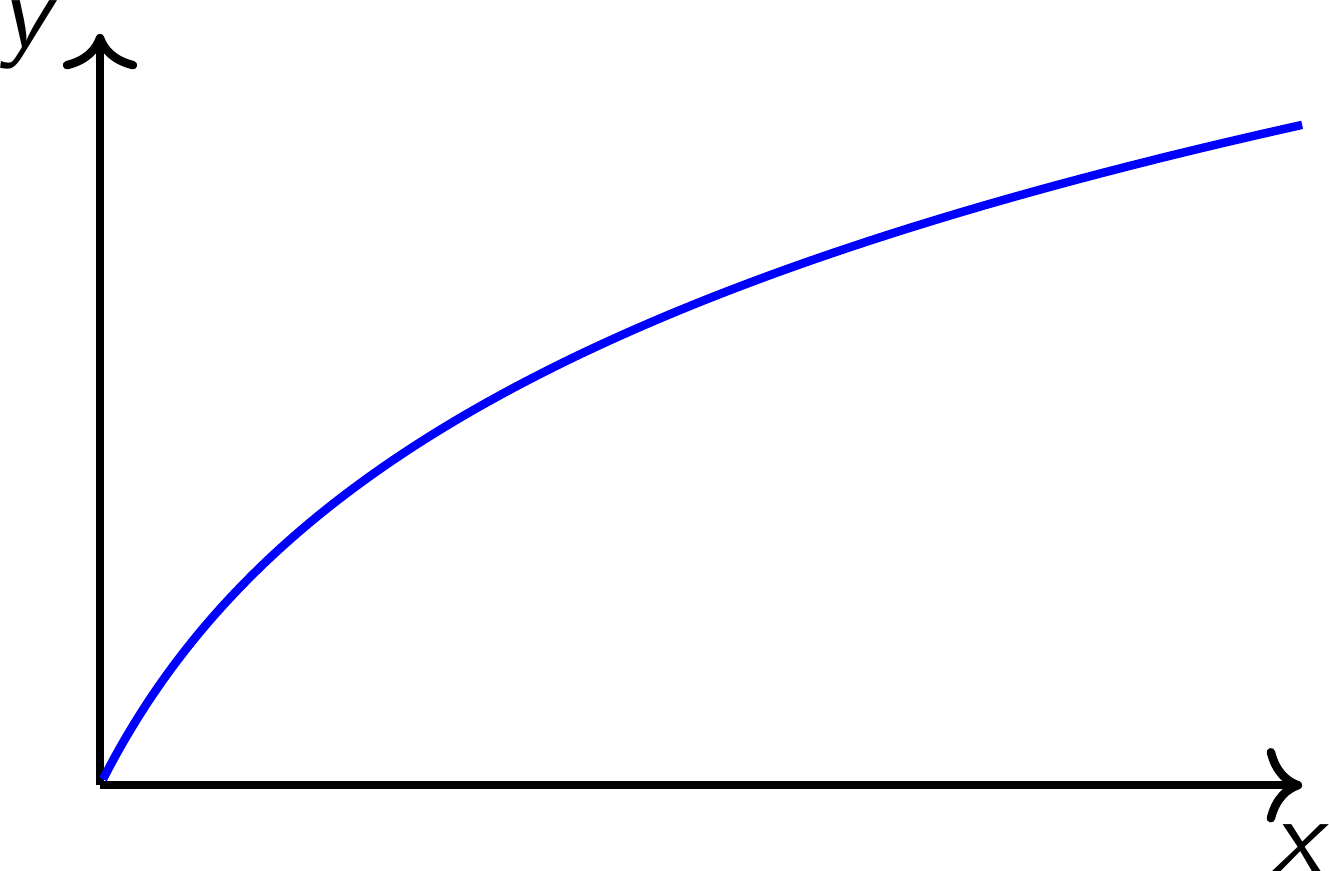
Isoquanten
Eine Isoquante ist die Menge aller möglichen Kombinationen von Faktoren, die genau ausreicht, um eine vorgegebene Menge des Outputs zu erzeugen
Jede Isoquante repräsentiert ein spezifisches Output-Niveau
Die Illustration im Zweifaktorenfall gibt es hier
Die Technische Rate der Substitution, also die Steigung der Isoquante, ist negativ und nimmt zu (bzw. der absolute Wert nimmt ab)
\[ TRS_{i,j} \equiv -\frac{MP_i}{MP_j}, \ \ \ \ \ \ \frac{\partial \ TRS_{i,j}}{\partial x_i}>0 \]
Die kurze und die lange Frist
Im Gegensatz zu Konsum-/Kaufentscheidungen können Produktionsfaktoren nicht immer sofort angepasst werden
Kurzfristig wird es Faktoren geben, die auf vorherbestimmten Niveaus fixiert sind, also zu Fixkosten führen
Installation bzw. Entfernen von Maschinen
Arbeitsgesetze und andere Langfrist-Verträge (z.B. Mietverträge)
Langfristig können alle Faktoren frei angepasst werden
Teamarbeit: Welche Faktoren kann Nvidia kurzfristig anpassen?
Skalenerträge
Oft hört man Sätze wie “Wir müssen das Geschäft schnell hochskalieren”, also alle Produktionsfaktoren und den Output erhöhen - warum?
Bestimmte Technologien bzw. Produktionsfunktionen implizieren, dass man produktiver wird, wenn man größer ist. Dann haben wir
steigendeSkalenerträge: \[ f(tx_1, tx_2) > tf(x_1, x_2), \ \ \ \ \ t > 1 \]Manchmal führen bspw. fixe Produktionsfaktoren wie Gebäude dazu, dass Skalenerträge
fallen\[ f(tx_1, tx_2) < tf(x_1, x_2), \ \ \ \ \ t > 1 \]Auch wenn Skalenerträge gerade langfristig u.a. durch Synergien steigen, kann man oft mittelfristig Produktionskapazitäten eins-zu-eins kopieren; dann sprechen wir von
konstantenSkalenerträgen \[ f(tx_1, tx_2) = tf(x_1, x_2), \ \ \ \ \ t > 1 \]
Teamarbeit: Wo sehen Sie im konkreten Fall Nvidia diese drei Arten von Skalenerträgen?
Beispiele zu Skalenerträgen
Nehmen wir an, die Produktionsfunktion lautet
\[ y=f(K,L)= K^{0.3}L^{0.7} \]
Welche Skalenerträge gibt es?
Antwort: Konstante Skalenerträge, da \(f(tK,tL)=(tK)^{0.3}(tL)^{0.7}=t \times K^{0.3}L^{0.7}\)
Und wenn \(f(K,L)=K^2+L^2\)?
Antwort: Steigende Skalenerträge, da \(f(tK,tL)=(tK)^2+(tL)^2= t^2 \times [K^2+L^2]\)
Das Verhalten einer Firma: Kostenminimierung
Kostenminimierungsproblem
Unser Ziel ist es, ein Marktangebot zu modellieren, das auf optimalen Entscheidungen von Unternehmen basiert
Dazu werden wir zunächst die Kostenfunktion einer Firma herleiten - anschließend kann sie entscheiden, welche Menge sie optimalerweise produziert
Das Kostenminimierungsproblem lautet \[
\min_{\boldsymbol{x}} \; \sum_{i} w_i x_i, \ \ \ u.d.N. \ \ f(\boldsymbol{x}) = y
\]
- wobei \(w_i\) die
Faktorpreiseangeben und \(y\) einer beliebigen Outputmenge entspricht
Hinweis: Faktorpreise nehmen Unternehmen aufgrund vollkommenen Wettbewerbs auf den Faktormärkten als gegeben hin – mehr dazu später!
Die Kostenfunktion
Das Ergebnis des Problems ist eine Kostenfunktion \[
c(\boldsymbol{w},y)
\]
- Die Kosten eines Unternehmens hängen also von den Faktorpreisen und dem produzierten Output ab
- Im Optimum müssen die relativen Kosten eines Faktors seinem relativen Grenzprodukt entsprechen (was wäre, wenn die relativen Kosten höher wären?)
- Formal haben wir also für alle Faktoren \(i\) und \(j\) \[ \frac{w_i}{w_j} = \frac{MP_i}{MP_j} \equiv - TRS_{i,j} \]
Isokostengerade
Um die Lösung intuitiv zugänglich zu machen, können wir wieder die Zielfunktion und die Nebenbedingung des Minimierungsproblems darstellen
- die Nebenbedingung – die Produktionsfunktion – wird durch die Isoquanten mit Outputniveau \(y\) abgebildet
- Auf Kostenseite haben wir im Zweifaktorenfall eine
Isokostengerademit Kostenniveau \(C\) \[ w_1 x_1 + w_2 x_2 = C \ \ \ \leftrightarrow \ \ \ x_2 = \frac{C}{w_2} - \frac{w_1}{w_2} x_1 \]
Im Optimum muss die Steigung der Isokostengerade der Steigung der Isoquanten entsprechen, \(-w_1/w_2=TRS_{i,j}\)
Hier geht es zur Illustration
Cobb-Douglas Beispiel mit zwei Faktoren
Das Kostenminimierungsproblem mit Produktionsfunktion \(f(x_1,x_2)=x_1^{\alpha}x_2^{\beta}\) lautet
\[ \min_{\boldsymbol{x}} \; w_1 x_1 + w_2 x_2, \ \ \ u.d.N. \ \ x_1^{\alpha}x_2^{\beta} = y \]
Die Bedingung erster Ordnung lautet (Lagrange oder Folie 16; Asterisk für optimale Lösung ausgelassen)
\[ \frac{w_1}{w_2}=\frac{\alpha x_1^{\alpha-1}x_2^{\beta}}{\beta x_1^{\alpha}x_2^{\beta-1}}=\frac{\alpha}{\beta}\frac{x_2}{x_1} \ \Leftrightarrow \ x_2 = \frac{\beta}{\alpha} \frac{w_1}{w_2} x_1 \]
Einsetzen in die Produktionsfunktion ergibt die Faktornachfragen
\[ y=x_1^{\alpha}\left (\frac{\beta}{\alpha} \frac{w_1}{w_2} x_1 \right)^{\beta} = x_1^{\alpha+\beta} \left (\frac{\beta}{\alpha}\frac{w_1}{w_2} \right)^{\beta} \ \Leftrightarrow \ x_1 = \left (\frac{\beta}{\alpha} \frac{w_1}{w_2} \right)^{-\frac{\beta}{\alpha+\beta}} y^{\frac{1}{\alpha+\beta}} \]
und
\[ x_2 = \frac{\beta}{\alpha} \frac{w_1}{w_2} x_1 = \frac{\beta}{\alpha} \frac{w_1}{w_2} \left (\frac{\beta}{\alpha} \frac{w_1}{w_2} \right)^{-\frac{\beta}{\alpha+\beta}} y^{\frac{1}{\alpha+\beta}} = \left (\frac{\beta}{\alpha} \frac{w_1}{w_2} \right)^{\frac{\alpha}{\alpha+\beta}} y^{\frac{1}{\alpha+\beta}} \]
Cobb-Douglas Beispiel mit zwei Faktoren (Fortsetzung)
Einsetzen in die Kostenfunktion ergibt schließlich
\[ C(w_1,w_2,y) = w_1 x_1 + w_2 x_2 = w_1 \left (\frac{\beta}{\alpha} \frac{w_1}{w_2} \right)^{-\frac{\beta}{\alpha+\beta}} y^{\frac{1}{\alpha+\beta}} + w_2 \left (\frac{\beta}{\alpha} \frac{w_1}{w_2} \right)^{\frac{\alpha}{\alpha+\beta}} y^{\frac{1}{\alpha+\beta}} = \\ \left [\frac{(\alpha+\beta)^{\alpha+\beta}}{\alpha^{\alpha}\beta^{\beta}} \right]^\frac{1}{\alpha+\beta} \left [w_1^{\alpha}w_2^{\beta} \right]^\frac{1}{\alpha+\beta} y^\frac{1}{\alpha+\beta} \]
Mit konstanten Skalenerträgen (\(\alpha+\beta=1\)) ist die Kostenfunktion linear im Output
\[ C(w_1,w_2,y) = \alpha^{-\alpha}\beta^{-\beta}w_1^{\alpha}w_2^{\beta} y \]
Kostenarten
Je nach Zeithorizont und Art der involvierten Faktoren kann man verschiedene Kostenarten unterscheiden:
Fixe Kostensind unabhängig vom Produktionsniveau und fallen auch ohne Output an; sie sind ein Phänomen der kurzen FristQuasifixe Kostensind unabhängig vom Outputniveau, entstehen aber nur, wenn das Unternehmen eine positive Outputmenge erzeugtVariable Kostensind Ausgaben, die sich mit der Produktionsmenge \(y\) verändernVerlorene Kostensind bereits angefallene, nicht wieder einholbare Ausgaben, die für zukünftige Entscheidungen irrelevant sind
Beispiel für Kostenarten
Teamarbeit: ordnen Sie gemeinsam die folgenden Kosten in der Tabelle ein
| Kosten | fix | quasi-fix | variabel | verloren |
|---|---|---|---|---|
| Büromiete (Jahresvertrag) | ||||
| Forschung und Entwicklung | ||||
| Serverwartung | ||||
| Marketing | ||||
| Produktionsanlagen | ||||
| Mitarbeiterschulungen | ||||
| Grafikprozessorenentwicklung | ||||
| Prototypen | ||||
| Komponenten (z.B. Chips) | ||||
| Strom für Produktionsstätten |
Nützliche Konzepte und Eigenschaften von Kostenfunktionen
Die Gesamtkosten eines Unternehmens sind \[ c(y) = F + c_v(y). \]
Für \(y > 0\) sind die Durchschnittskosten (Average Costs) \[
AC(y) = \frac{F}{y} + \frac{c_v(y)}{y} = AFC(y) + AVC(y).
\]
\(AFC(y)\) - Durchschnittliche Fixkosten (Average Fixed Costs)
\(AVC(y)\) - durchschnittliche variable Kosten (Average Variable Costs)
Grenzkosten (Marginal Costs) sind die Änderungsrate der Produktionskosten bei einer Änderung der Outputmenge \[
MC(y) = \frac{\partial c(y)}{\partial y}
\]
Teamarbeit: Wie lauten die Grenz- und Durchschnittskosten mit Cobb-Douglas (Folie 19)? Mit konstanten Skalenerträgen?
Grafische Illustration von Kostentypen
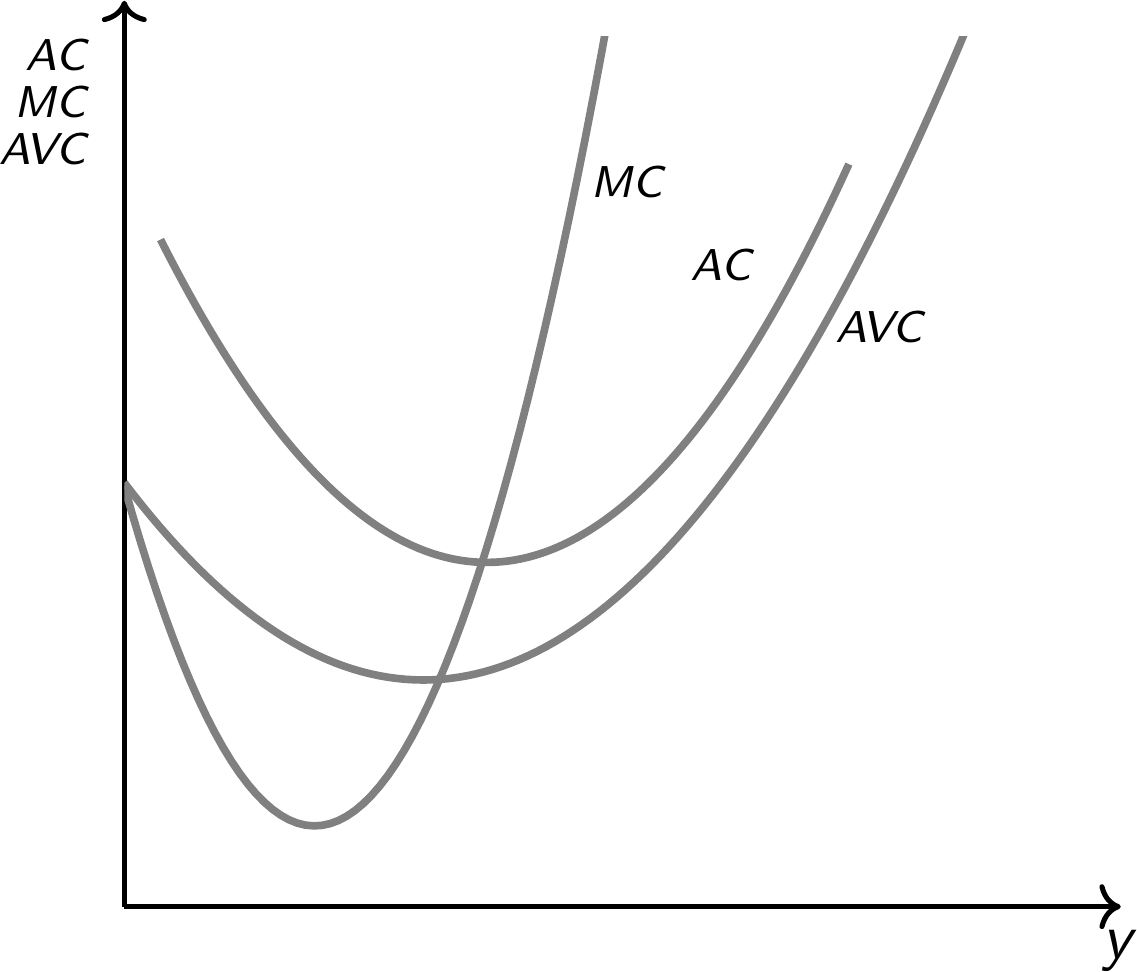
\(MC(y) = \frac{\mathrm{d}}{\mathrm{d} y} (F + c_v(y))\), \(AC(y) = \frac{F+c_v(y)}{y}\) und \(AVC(y) = \frac{c_v(y)}{y}\)
Das Verhalten der Unternehmung: das individuelle Angebot
Gewinnmaximierung
Dass Unternehmen ihre Kosten minimieren wollen, erscheint zunächst als plausibel und unkontrovers
Um Angebotsfunktionen und letztlich ein Marktangebot zu modellieren, nehmen wir zudem Gewinnmaximierung in der betrachteten Periode an
- Realistisch? Alternativ könnten Marktanteile, philanthropische Ziele (viele non-profits), individuelle Interessen (Familienunternehmen) oder sogar Schäden (hacker, fake news) im Mittelpunkt stehen
- Realistisch? Unternehmen müssen investieren und planen für unterschiedliche Zeithorizonte
- Gewinnmaximierung ist eine gute Approximation, insbesondere für börsennotierte Unternehmen wie Nvidia, und die Frist wird durch die Kostenfunktion abgebildet
Aber was ist der ökonomische Gewinn?
- Alle Umsätze abzüglich aller Faktorentlohnungen zu Marktpreisen
Das Marktumfeld
Für die Angebotsseite benötigen wir außerdem Annahmen darüber, wie Unternehmen mit Kunden interagieren
- Für unseren Benchmark nehmen wir an, dass Unternehmen keinerlei
Marktmachtbesitzen (dies ist eine der problematischen Annahmen, die wir später in der Vorlesung genau unter die Lupe nehmen)
- Auf Output- und Faktormärkten sind sie
Preisnehmerund bieten zum jeweiligen Preis eine bestimmte Menge an oder fragen bestimmte Mengen nach
Vollkommener Wettbewerbist eine Möglichkeit, diese Annahme zu begründen
Teamarbeit: Welche Güter- oder Dienstleistungsmärkte sind mit diesem Modell gut oder weniger gut beschrieben?
Herleitung des kurzfristigen individuellen Angebots
Das Gewinnmaximierungsproblem lautet unter diesen Annahmen \[
\max_{y \geq 0} \pi(y) = py - c(y)
\]
Die notwendige Bedingung erster Ordnung ist \[ \underbrace{p}_{\text{Grenzerlös} \\ \ \ \ \ \ MR} \leq \underbrace{ \left. \frac{\partial c(y)}{\partial y}\right |_{y^*}}_{\text{Grenzkosten} \\ \ \ \ \ \ \ \ MC} \underbrace{= \left. \frac{\partial c_v(y)}{\partial y}\right|_{y^*}}_{\text{kurzfristig}} \]
Unternehmen vergleichen also Grenzerlös (Marginal Revenue) mit Grenzkosten
Verdiene ich mit der nächsten produzierten Einheit mehr als sie kostet? Dann muss ich mehr produzieren und \(y^*\) ist kein Optimum
Verdiene ich weniger? Dann muss ich mein Angebot weiter reduzieren
Hinweise zum individuellen Angebot
Beachte: die B.e.O. ist eine schwache Ungleichung, denn es kann optimal sein, nichts zu produzieren
Beachte: die B.e.O. ignoriert etwaige Fixkosten; es muss daher zusätzlich eine Stilllegungsbedingung gelten (\(y^{*,s}\) ist der optimale short run Output) \[
\underbrace{py^{*,s} - c_v(y^{*,s}) - F}_{\text{Gewinn bei } y^{*,s}\geq 0} \geq \underbrace{-F}_{\text{Gewinn bei } y^{*,s}=0} \ \ \ \leftrightarrow \ \ \ p \geq \frac{c_v(y^{*,s})}{y^{*,s}} = AVC(y^{*,s})
\]
Wenn der Preis nicht einmal die durchschnittlichen variablen Kosten deckt, sollte man ebenfalls die Produktion einstellen
Unternehmen bieten also nur an, wenn \(MC(y)>AVC(y)\), also im steigenden Bereich der MC-Kurve oberhalb der AVC-Kurve auf Folie 23
Die (strikt steigende) individuelle Angebotskurve ist also
\[ y = \begin{cases} MC^{-1}(p), & \text{falls } \ \ y \geq AVC^{-1}(p), \\ 0, & \text{andernfalls.} \end{cases} \]
Das Branchenangebot
Kurzfristiges Branchenangebot
Bei \(n\) Unternehmen im Markt ist die Angebotskurve
\[ S(p) = \sum_{i=1}^n y_i(p). \]
Dieses Marktangebot steigt typischerweise im Preis
Da alle Unternehmen annahmegemäß den gleichen Preis verlangen müssen, um zu verkaufen, haben wir u.U. eine spannende Situation
Liegt ein beliebiger Preis \(p'\) über den Durchschnittskosten \(AC_i(y_i(p'))\) eines Unternehmens \(i\), so macht dieses einen
ökonomischen GewinnLiegt er darunter, macht es einen Verlust
Langfristiges Branchenangebot: Eintritt und Austritt
Diese Situation entsteht kurzfristig, da es keinen Marktein- oder -austritt gibt
- Das langfristige Angebot sollte daher nicht nur die langfristige Kostenfunktion, sondern auch Ein- und Austritt berücksichtigen
Gibt es keine Markteintrittsbarrieren, werden so lange Unternehmen eintreten bzw. Produktionskapazitäten geschaffen, bis alle Gewinne auf Null gedrückt werden
Die Angebotskurve wird somit flacher bzw. elastischer
Produzieren alle Unternehmen mit der gleichen Technologie, ist das langfristige Angebot flach bei \(p=AC(y^{min})\), wobei \(y^{min}\) das Minimum der Durchschnittskostenkurve beschreibt
Nützliches Konzept: Produzentenrente
Analog zur Konsumentenrente definieren wir die Produzentenrente
Wie jede ökonomische Rente entspricht sie der Differenz zwischen Preis und den Opportunitäts- bzw. Produktionskosten
Im Fall eines Unternehmens also Umsatz minus variable Produktionskosten (die fixen Kosten variieren nicht mit der produzierten Menge, sind also unerheblich)
Da letztere einfach dem Integral der Grenzkosten bis zur Produktionsmenge entsprechen, ist die Produzentenrente die Fläche oberhalb der inversen Angebotskurve und unterhalb des relevanten Preises
Zur grafischen Darstellung geht es hier
Wiederholungsfragen
Inwiefern ist eine Unterscheidung zwischen kurzer und langer Frist für Unternehmen wichtig?
Laden Sie die Kostenminimierungsgrafik. Erklären Sie in Ihren Worten, welche Kurven zu sehen sind, welche Interpretation sie haben, und wie man mit ihrer Hilfe die Kostenfunktion eines Unternehmens finden kann.
Laden Sie die Marktdarstellung.
Machen Sie die Angebotskurve elastischer. Repräsentiert diese Kurve nun ein langfristigeres Angebot?
Erklären Sie den Begriff Produzentenrente in eigenen Worten. Blenden Sie diese in der Grafik ein und ergründen Sie, wovon die Höhe der Produzentenrente abhängt.
Widgets
Kostenminimierung
Zurück zu “Isoquanten” oder “Isokostengerade”
Markt
Zurück zu “Produzentenrente”