Mikroökonomie

Vorlesung 1: Die Nachfrageseite



Prof. Frank Pisch PhD

Motivation

Nachfrage in den Medien

manager magazin

tagesschau.de

Aggregierte Nachfrage

destatis

Um Märkte zu verstehen, brauchen wir ein Modell der Nachfrage

  • Zusammen mit dem Angebot bestimmt sie Preise und Konsum

  • Sie sagt uns, wer wie viel und zu welchem Preis konsumiert…

  • … und somit wie es um die Konsumentenwohlfahrt steht

Zentrale Elemente der individuellen Nachfrage

Marktnachfrage wird (heutzutage) immer auf individuelle Nachfragen, also auf das Entscheidungsverhalten von einzelnen Konsumenten zurückgeführt.

In der Einführungsvorlesung haben wir uns Ihre Nachfrage nach Smartphones angesehen. Wovon hängt sie ab?

  • Ihr Bedarf bzw. Ihre Wünsche

  • Ihr (knappes) Budget und der Preis

  • Ob Sie beides gut in Einklang bringen können

In der VWL haben wir dafür spezielle Namen, aber die Interpretation ist gleich

  • Präferenzen

  • Budget

  • Rationalität und insbesondere Nutzenmaximierung

Überblick und Ressourcen

Ziele

  • Verstehen, wie wir in der VWL über Präferenzen und Budgets nachdenken

  • Analysieren, wie optimale Nachfrageentscheidungen und eine aggregierte Marktnachfrage zustande kommen

  • Einige zentrale Konzepte entwickeln und verstehen

    • Insbesondere Wohlfahrtsmaße

Ressourcen

  • (Einige) Kapitel im Varian: 2 - 8, 14, 15

  • Interaktive Diagramme

  • YouTube und KI-Tools

Budget

Notation und Zweigüterfall

Betrachten wir zwei Güter – ohne Einschränkung der Allgemeinheit

  • Waren, Dienstleistungen, andere Dinge wie frische Luft

Ein Güterbündel ist \(\mathbf{x} = (x_1,x_2)\), wobei \(x_i\geq 0\) die konsumierte  Menge darstellt

  • Fette Buchstaben bezeichnen immer Vektoren, also Listen mit Einträgen – hier für Gut 1 und Gut 2

  • Beispiel: Gut 1 ist ein Smartphone, Gut 2 ein Tablet; zwei Güterbündel \(\mathbf{x}\) und \(\mathbf{y}\) könnten sein:

\[ \mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ \ \ \ \ \mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} 4 \\ 8 \end{pmatrix} \]

Die dazugehörigen Preise \(p_i\) pro Einheit sind für Konsumenten gegeben und einheitlich

Das verfügbare Budget ist \(m\)

Budgetbeschränkung: Was kann man sich leisten?

Die Budgetmenge enthält alle Güterbündel, die bei den aktuellen Preisen erschwinglich sind \[ \mathbf{x}^{T}\mathbf{p} = p_1 x_1 + p_2 x_2 \leq m \]

Sie wird durch die Budgetgerade abgegrenzt, also die Menge aller Güterbündel, die das Budget vollkommen ausschöpfen

\[ x_2 = \frac{m}{p_2}-\frac{p_1}{p_2}x_1 \]

Die Steigung zeigt an, mit welcher Rate die beiden Güter auf der Budgetgerade füreinander substituiert werden können, also die Opportunitätskosten

  • Opportunitätskosten sind allgemein die ökonomischen Kosten einer Entscheidung, also der Wert der besten ungenutzten Alternative

  • Im Kontext der Budgetgeraden:

\[ \frac{\mathrm{d}x_2}{\mathrm{d}x_1} = -\frac{p_1}{p_2} \]

Die grafische Illustration befindet sich hier

Opportunitätskosten im Fokus

Opportunitätskosten sind eines der wichtigsten Konzepte in den Wirtschaftswissenschaften (und darüber hinaus)

Nehmen wir an, Sie haben \(m=10\), \(p_{\text{Smartphone}}=2\) und \(p_{\text{Tablet}}=4\)

  • Das Güterbündel (1 Tablet, 3 Smartphones) schöpft das Budget aus

  • Man kann entlang der Budgetgerade zwei Smartphones abgeben, um ein Tablet zu bekommen

  • Die Opportunitätskosten eines Tablets sind immer zwei Smartphones

Einige allgemeinere Beispiele:

  • Studieren und insbesondere ein Doktorat haben hohe Opportunitätskosten: entgangenes Einkommen und Erfahrung

  • Jede Ausgabe – zum Beispiel eine Investition – hat Opportunitätskosten in Höhe des „Zinses“, den das Geld angelegt erwirtschaftet hätte

  • DIY (z.B. Heimwerkeln) ist immer eine Abwägung, da die eigene Zeit auch anders genutzt werden kann

    • Putzhilfe in der WG??

Arbeitsteilung und Spezialisierung nach komparativem Vorteil

Präferenzen und Nutzen

Präferenzen: Was möchte man haben?

In der VWL modellieren wir Bedürfnisse und Wünsche mithilfe von Präferenzen

Beispiel: Gut 1 ist ein iPhone 17, Gut 2 ein Samsung S25

  • Wir vergleichen zwei Güterbündel \(\mathbf{x} = (x_1,x_2) = (1,0)\) und \(\mathbf{y} = (y_1,y_2) = (0,1)\)

Manche von Ihnen bevorzugen strikt Apple; dann schreiben wir \[ \mathbf{x} \succ \mathbf{y} \ \ \ \ \ \Leftrightarrow \ \ \ \ \ (1,0) \succ (0,1) \]

  • Und wenn ich Ihnen noch ein S25 oben drauf packe – Güterbündel \(\mathbf{z}=(0,2)\)? Dann sind Sie vielleicht indifferent \[ \mathbf{x} \sim \mathbf{z} \ \ \ \ \ \Leftrightarrow \ \ \ \ \ (1,0) \sim (0,2) \]
  • Abschließend gibt es noch die schwache Präferenz: Das Samsung Handy wird zumindest nicht präferiert \[ \mathbf{x} \succsim \mathbf{y} \ \ \ \ \ \Leftrightarrow \ \ \ \ \ (1,0) \succsim (0,1) \]

Alle Operatoren sind Präferenzrelationen, also logische Operatoren, die eine Ordnung (ein „ranking“) von Güterbündeln darstellen

„Vernünftige“ Präferenzen

Wir nehmen an, dass Präferenzen bestimmte Eigenschaften erfüllen, sodass sie auf eine bestimmte Weise „wohlverhalten“ sind:

  1. vollständig („\(\lor\)“ ist das logische „oder“, „\(\forall\)“ bedeutet „für alle“) \[ \forall \ \mathbf{x}, \mathbf{y}: \ \ \ \ \ \ \mathbf{x} \succsim \mathbf{y} \ \ \lor \ \ \mathbf{y} \succsim \mathbf{x} \]

  2. reflexiv \[ \forall \ \mathbf{x}: \ \ \ \ \ \ \mathbf{x} \succsim \mathbf{x} \]

  3. transitiv („\(\land\)“ ist das logische „und“) \[ \forall \ \mathbf{x}, \mathbf{y}, \mathbf{z}: \ \ \ \ \ \ \mathbf{x} \succsim \mathbf{y} \ \ \land \ \ \mathbf{y} \succsim \mathbf{z} \ \ \implies \ \mathbf{x} \succsim \mathbf{z} \]

  4. monoton \(\leftrightarrow\) keine Sättigung \[ x_i \geq y_i \ \ \ \ \forall \ i \ \ \implies \ \ \mathbf{x} \succsim \mathbf{y} \]

  5. stetig

Teamarbeit: wie realitätsnah sind diese Annahmen?

Nützliche Beschreibung: Die Nutzenfunktion

Optimale Entscheidungen nur mithilfe von Präferenzrelationen zu finden ist schwierig…

Können wir vielleicht jedem Bündel einen Wert zuweisen, sodass die Präferenzen „repräsentiert“ werden?

  • Mit unseren Annahmen ist dies garantiert (Debreu’s Nutzen-Representationstheorem)!

  • Wir haben dann sogar wohlverhaltene Funktionen

Diese  Nutzenfunktionen werden zumeist als \(u(\mathbf{x}) = u(x_1,x_2)\) notiert



Teamarbeit: Gehen Sie zurück auf Folie 12 und finden Sie Funktionen, die die jeweiligen Präferenzen repräsentieren könnten!

Kardinaler vs Ordinaler Nutzen

Sie haben sicher festgestellt: die gleichen Präferenzen können durch unendlich viele Funktionen dargestellt werden

Nutzenfunktionen sind also immer ordinal: Sie geben nur Reihenfolgen an, und absolute (kardinale) Unterschiede im Nutzenwert haben keine Bedeutung

Somit können wir immer monotone Transformationen auf Nutzenfunktionen anwenden, und die resultierende Funktion repräsentiert die selben Präferenzen!

Das steht in großem Kontrast zur Volkswirtschaftslehre in den Anfängen: im 19. Jahrhundert war „Nutzen“ messbar und absolut…

Beispiele für Nutzenfunktionen

  • Perfekte Substitute

\[ u(\mathbf{x}) = x_1 + x_2 \]

  • Perfekte Komplemente

\[ u(\mathbf{x}) = \mathrm{min}\{x_1,x_2\} \]

  • Cobb-Douglas

\[ u(\mathbf{x}) = x_1^{\alpha}x_2^{1-\alpha} \ \ \ \ \text{with} \ \alpha \in (0,1) \]

  • Quasilineare Präferenzen

\[ u(\mathbf{x}) = v(x_1) + x_2, \ \ \ \ \ \text{mit} \ \ \ \ v'>0, \ \ v''<0 \]

Teamarbeit: Beschreiben Sie das Verhalten dieser Präferenzen in Worten!

Weitere Konzepte und das Verhalten von Nutzenfunktionen

Überblick

In diesem Teil lernen wir zwei zentrale Konzepte kennen, die uns helfen werden, Nutzenfunktionen besser zu verstehen und später die Nachfrage herzuleiten.

  • Grenznutzen

  • Indifferenzkurven

Auch wenn beide Konzepte zunächst formalistisch anmuten, können wir sie mithilfe von Beispielen leicht verstehen.

Oktoberfest

DALL-E

Grenznutzen ist positiv, aber abnehmend!

DALL-E

Indifferenzkurven geben an, in welchen Verhältnissen Güter konsumiert werden können, ohne dass sich das Nutzenniveau ändert.

Zentrales Konzept: Grenznutzen

Betrachten wir den Fall eines einzigen Gutes, sodass der Nutzen \(u=u(x)\) ist

Motivation: Wie finden wir das beste Güterbündel?

  • Starten wir bei einer beliebigen Konsummenge \(x=k\). Wollen wir mehr oder weniger konsumieren?

  • Wenn der zusätzliche Nutzen der nächsten Einheit größer als der Preis (gemessen in Nutzen) ist, wollen wir mehr; wenn er niedriger ist, wollen wir den Konsum reduzieren.

Der Grenznutzen eines Gutes \(i\) (Marginal Utility), \[ \frac{\partial u(\mathbf{x})}{\partial x_i} \equiv MU_i(\mathbf{x}), \] ist der marginale Zusatznutzen, wenn man die Menge um eine infinitesimale Einheit erhöht.

Hinweise:

  • Der Grenznutzen ist immer parziell

  • Typischerweise fällt der Grenznutzen eines Gutes, wenn man mehr konsumiert

Zentrales Konzept: Indifferenzkurven

Um das beste Güterbündel – und damit die Nachfrage – zu finden, werden wir ein sehr nützliches Konzept nutzen: Indifferenzkurven

  • Sie sind Mengenscharen aller Güterbündel, die den gleichen Nutzenwert erzeugen; also solche, zwischen denen ein:e Konsument:in indifferent ist:

\[ \{\mathbf{x}|u(\mathbf{x})=\bar{u}\} \]

  • Ihre Form zeigt uns, wie wir substituieren, also freiwillig von einem Gut weniger und von anderen mehr konsumieren würden

Die grafische Illustration befindet sich hier

Steigung der Indifferenzkurve: die Grenzrate der Substitution

Das beste Güterbündel in Abhängigkeit von Preisen und Budget – also die Nachfrage – liegt auf der höchsten Indifferenzkurve, auf der mind. ein Güterbündel in der Budgetmenge liegt

  • Es wird also ein Tangenzialpunkt gesucht: Im Optimum ist die Steigung der Indifferenzkurve genauso groß wie die Steigung der Budgetgeraden

Die Steigung der Indifferenzkurve wird als  Grenzrate der Substitution bezeichnet (marginal rate of substitution)

  • Für ein beliebiges Nutzenniveau \(\bar{u}\) und eine Nutzenfunktion für zwei Güter \(u(x_1,x_2)\):

\[ \mathrm{d} u(x_1,x_2) = \mathrm{d} \bar{u} = 0 = \frac{\partial u}{\partial x_1} \mathrm{d} x_1 + \frac{\partial u}{\partial x_2} \mathrm{d} x_2 \Leftrightarrow \]

\[ \frac{\mathrm{d} x_2}{\mathrm{d} x_1} = \underbrace{- \frac{\frac{\partial u}{\partial x_1}}{\frac{\partial u}{\partial x_2}}}_{\text{Grenzrate der Substitution}} \equiv - \frac{MU_1}{MU_2} \equiv MRS_{1,2} \]

Eigenschaften der MRS

Die MRS ist bei differenzierbaren Nutzenfunktionen typischerweise negativ

  • Wenn man von einem Gut mehr konsumiert, kann man ohne Nutzenverlust weniger von einem anderen konsumieren

Sie gibt den „Wechselkurs“ an, zu dem Konsument:innen bereit sind, Güter füreinander auszutauschen

Bei schwach konvexen Präferenzen fällt die MRS nicht; bei strikt konvexen Präferenzen steigt sie

  • D.h. \(|MRS_{i,j}|\) nimmt typischerweise schwach in \(x_i\) ab

  • Man muss also immer mehr von einem Gut aufgeben, um den Nutzen durch Konsum des anderen Gutes konstant zu halten

Individuelle Nachfrage

Überblick

In diesem Teil leiten wir uns die individuelle Nachfrage als Funktion des Budgets und der Güterpreise her

  • Zunächst mithilfe des Lagrange Ansatzes

  • Anschließend bilden wir Intuition mithilfe der grafischen Lösung im Zweigüterfall

Im folgenden Schritt können wir über Konsument:innen hinweg aggregieren, um die Marktnachfrage zu erhalten

Der Lagrange Ansatz

Das Optimierungsproblem ist, Güterbündel zu wählen, die den Nutzen unter Einhaltung der Budgetbedingung maximieren:

\[ \mathrm{max}_{\mathbf{x}} \ \ u(\mathbf{x}) \ \ \ \ \ \text{u.d.N.} \ \ \ \ \mathbf{x}^{T}\mathbf{p} \leq m \]

  • Wir verwenden die Lagrange-Methode mit Multiplikator \(\lambda\): \[ \mathrm{max}_{\mathbf{x},\lambda} \ \ \ \mathscr{L} = u(\mathbf{x}) + \lambda (m-\mathbf{x}^{T}\mathbf{p}) \]
  • Die notwendigen Bedingungen erster Ordnung geben uns ein Gleichungssystem, das wir für \(\mathbf{x}^*, \ \lambda^*\) lösen können

\[ \left. \frac{\partial u(.)}{\partial x_i} \right |_{\mathbf{x^*}} = MU_i|_{\mathbf{x^*}} = \lambda^* p_i \ \ \ \ \ \ \ \forall i \]

\[ m = \mathbf{x^*}^{T} \ \mathbf{p} \]

  • Beachte: Im Zuge dieser Veranstaltung kennzeichnen wir alle optimalen Lösungen mit einem Asterisk \(*\)

Optimale Nachfrage

Dividieren wir die Bedingungen erster Ordnung für zwei Güter \(i\) und \(j\) durcheinander und multiplizieren mit \(-1\), erhalten wir einen richtig nützlichen Ausdruck: \[ \underbrace{ \left. -\frac{\frac{\partial u(.)}{\partial x_i}}{\frac{\partial u(.)}{\partial x_j}} \right |_{\mathbf{x^*}} = \left. - \frac{MU_i}{MU_j} \right |_{\mathbf{x^*}}}_{\text{Grenzrate der Substitution}} = \underbrace{-\frac{p_i}{p_j}}_{\text{Steigung der Budgetgeraden}} \]

Wie schon antizipiert, erfüllt das optimale Güterbündel die oben erwähnte Tangenzialbedingung von Indifferenzkurve und Budgetgerade

Weitere Intuition: Nehmen wir an, dass für ein Güterbündel \((x_1', x_2')\) gilt:

\[-MRS(x_1',x_2')>p_1/p_2.\]

  • Der relative Grenznutzen von Gut 1 ist somit hoch im Vergleich zum relativen Preis. Somit möchte man mehr von Gut 1 und weniger von Gut 2 konsumieren.

  • Man befindet sich auf einer Indifferenzkurve in einem Bereich, wo sie steiler als die Budgetgerade ist; somit muss relativ mehr von Gut 1 konsumiert werden, sodass die \(|MRS_{1,2}|\) fällt

  • Für Fortgeschrittene: \(\lambda^*\) ist der Grenznutzen des Einkommens bzw. sein Schattenpreis; eine marginale Budgeterhöhung führt zu \(\lambda^*\) mehr Nutzen

Verifizieren Sie das bitte in der grafischen Analyse.

Beispiel: Cobb-Douglas

Mit einer expliziten Nutzenfunktion können wir nun die individuelle Nachfrage ausrechnen:

  • Nehmen wir Cobb-Douglas Präferenzen an, also

\[ u(x_1,x_2)=x_1^{\alpha}x_2^{1-\alpha} \ \ \ \ \ \text{mit} \ \alpha \in (0,1) \]

  • Die beiden relevanten Gleichungen sind also

\[ -\frac{\alpha}{1-\alpha} \frac{x_2^*}{x_1^*} = - \frac{p_1}{p_2} \ \ \ \Leftrightarrow \ \ \ x_2^* = \frac{1-\alpha}{\alpha} \frac{p_1}{p_2}x_1^* \] \[ m=x_1^*p_1 + x_2^*p_2 \]

  • Durch Lösung des Gleichungssystems erhalten wir die Nachfragefunktionen

\[ x_1^* \equiv x_1(p_1,p_2,m) = \frac{\alpha \ m}{p_1}, \ \ \ x_2^*\equiv x_2(p_1,p_2,m) = \frac{(1-\alpha) \ m}{p_2} \]

  • Mit Cobb-Douglas Präferenzen gibt man konstante Anteile \(\alpha\) für Gut 1 und Gut 2 aus; bei \(\alpha=0.5\) also jeweils das halbe Budget

Nota bene: wir vernachlässigen Randlösungen und Bedingungen zweiter Ordnung.

Eigenschaften der individuellen Nachfrage

Exploration: Veränderung des Einkommens

Teamarbeit: Gehen Sie zum Nutzenmaximierung Widget und spielen Sie mit dem Einkommensparameter herum

  • Wie verändern sich Budgetgerade und Indifferenzkurven?

  • Wie verändert sich das Nachfragebündel?

  • Wie sieht das ganze mit unterschiedlichen Präferenzen aus?

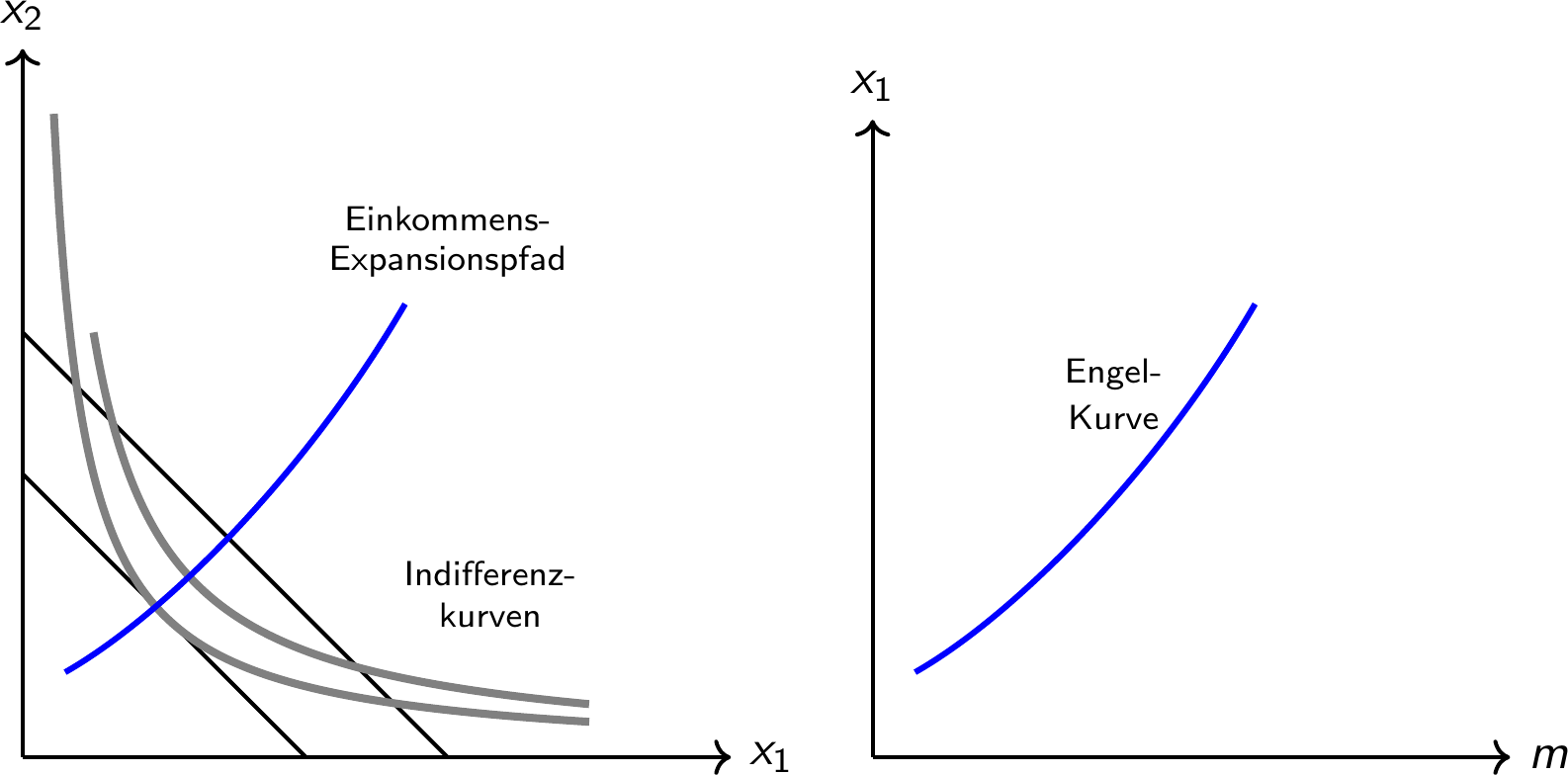
Einkommens-Expansionspfade, Engel-Kurven und Gütertypen

Viele Güter sind normal: bei höherem Budget wird mehr konsumiert

  • Der Einkommens-Expansionspfad im Zweigüterfall und die Engel-Kurve haben eine monoton positive Steigung (siehe nächste Folie)

Einige Güter sind (abschnittsweise) inferior: die Nachfrage reduziert sich bei höherem Budget

  • Dies betrifft vor allem Güter mit niedriger Qualität

  • Die Engel-Kurve fällt und der Einkommens-Expansionspfad ist „gewunden“

Steigt die Nachfrage schneller als das Budget (im Sinne einer Elastizität), spricht man von einem Luxusgut; steigt sie langsamer, ist es ein notwendiges Gut

Grafik: Einkommens-Expansionspfad und Engel-Kurve

Nach Varian, Abbildung 6.3

Exploration: Veränderung der relativen Preise

Teamarbeit: Gehen Sie wiederum zum Nutzenmaximierung Widget und spielen Sie mit einem der Preise herum

  • Wie verändern sich Budgetgerade und Indifferenzkurven?

  • Wie verändert sich das Nachfragebündel?

  • Wie sieht es mit unterschiedlichen Präferenzen aus?

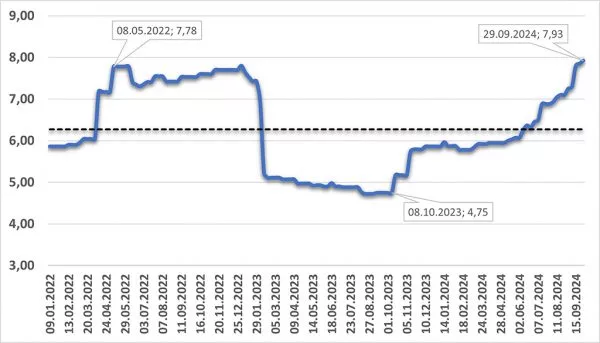
Anwendung: Butterpreise

EUR/kg, Landesbetrieb Landwirtschaft Hessen, Süddeutsche Butter- und Käsebörse

Anwendung: Gebrauchtwagen

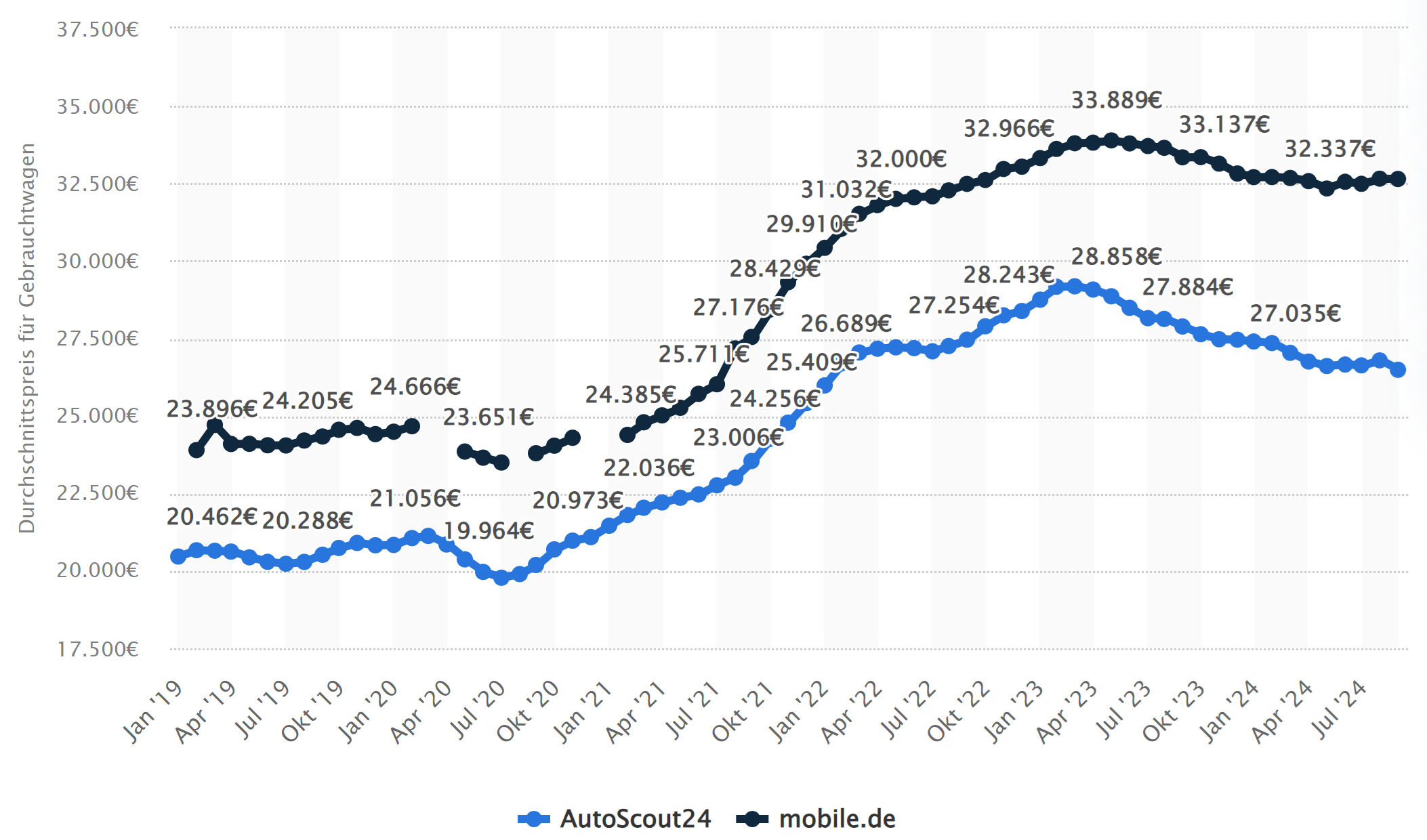
Image

de.statista.com

Die Slutsky Zerlegung

Eine Preissteigerung hat immer zwei Effekte:

  1. Substitutionseffekt: Andere Güter werden relativ billiger, sodass Konsumenten ‚wegsubstituieren‘
  • dieser Effekt wirkt immer in diese Richtung
  1. Einkommenseffekt: Das Preisniveau steigt insgesamt an, sodass das reale Budget kleiner wird
  • dieser Effekt kann, wie oben gesehen, den Konsum erhöhen oder senken

Mathematisch kann man leicht die Slutsky Identität herleiten

\[ \underbrace{ \left.\frac{\partial x_1(p_1,p_2,m)}{\partial p_1}\right|_{(\bar p_1,\bar p_2,\bar m)} }_{\text{Gesamteffekt (?)}} = \underbrace{ \left.\frac{\partial x_1^S(p_1,p_2,\bar x_1,\bar x_2)}{\partial p_1}\right|_{(\bar p_1,\bar p_2)} }_{\text{Substitutionseffekt }\leq 0} - \underbrace{ \bar x_1 \left.\frac{\partial x_1(p_1,p_2,m)}{\partial m}\right|_{(\bar p_1,\bar p_2,\bar m)} }_{\text{Einkommenseffekt (?)}} \]

  • Der Überstrich zeigt ursprüngliche Werte an

  • \(x_i^S(p_1,p_2,\bar x_1,\bar x_2)\): Nachfrage nach Gut \(i\) wenn das Budget ausgeglichen wird, man sich das alte Güterbündel also noch leisten kann (d.h. mit \(m^S(p_1,p_2) = p_1\bar x_1+p_2\bar x_2\)): \[ x_1^S(p_1,p_2,\bar x_1,\bar x_2) = x_1\left(p_1,p_2,m^S(p_1,p_2)\right) \]

Giffen Güter

Könnte es sein, dass ein Gut stärker nachgefragt wird, wenn sein Preis steigt?

Haben Sie Beispiele?

Slutsky zeigt uns: Prinzipiell kann der Einkommenseffekt so stark sein, dass er den Substitutionseffekt überkompensiert; solche Güter heißen  Giffen Güter

Empirische Evidenz

  • Jensen/Miller (2008): Reis und Fleisch Konsum extrem armer Menschen

    • Feldexperiment in der Provinz Hunan: randomisierte Zuteilung von Gutscheinen für Reis an Haushalte

    • Reiskonsum fiel, insbesondere in Haushalten mit einem „mittelhohen“ Einkommen

Substitute und Komplemente

Bei den Präferenzen haben wir bereits informell von Substituten und Komplementen gesprochen, dies aber nicht definiert

  • Gut \(i\) ist ein Brutto-Substitut (Brutto-Komplement) für Gut \(j\neq i\), wenn

\[\frac{\partial x_i(\mathbf{p},m)}{\partial p_j} > 0 \ \ (<0)\]

  • Der Substitutionseffekt ist größer (kleiner) als der Einkommenseffekt

  • Bei Netto-Substituten (-Komplementen) ist der Substitutionseffekt positiv (negativ)

Beispiel: Bei Cobb-Douglas Präferenzen sind Güter weder Brutto-Substitute noch Brutto-Komplemente (\(i \neq j\)):

\[ \frac{\partial x_i(\mathbf{p},m)}{\partial p_j} = \frac{\partial \alpha_i m/p_i}{\partial p_j}=0 \]

Sie sind jedoch Netto-Substitute, da der Substitutionseffekt positiv ist

Die Marktnachfrage, Elastizitäten und Konsumentenwohlfahrt

Aggregation

Um zur Marktnachfrage zu gelangen, ermitteln zunächst die individuelle Nachfrage

Bei normalen Gütern fällt diese Funktion, wie Sie bei Ihren Explorationen bereits feststellen konnten

Die Marktnachfrage von \(n\) Konsument:innen ergibt sich dann als die Summe aller individuellen Nachfragen:

\[ X_i(\mathbf{p},\mathbf{m}) \equiv \sum_{c=1}^{n} x_i^c(\mathbf{p},m^c) \]

Wenn die Präferenzen aller Konsument:innen bestimmte Bedingungen erfüllen, können wir vernachlässigen, dass die Marktnachfrage von der Verteilung der Einkommen abhängt

  • Dann sprechen wir von einem repräsentativen Konsumenten mit Budget \(M=\sum m^c\), der sich wie die Gesamtheit der Konsumenten verhält

Übersicht: Einige zentrale Konzepte

Die Eigenschaften der Nachfragefunktion spielen eine zentrale Rolle in der VWL

  • Preissetzung von Unternehmen

  • Marktreaktionen auf Steuern, Subventionen, Friktionen oder Schocks

  • Wohlfahrtseffekte

Um das besser zu verstehen, nutzen wir drei wichtige Konzepte

  • Preiselastizität

  • Einkommenselastizität

  • Konsumentenrente

Die Preiselastizität der Marktnachfrage

Oft sprechen wir aus verschiedenen Gründen von preiselastischer oder preisUNelastischer Nachfrage

  • Unternehmen messen bspw. ihre Marktmacht daran, wie sensitiv ihre Kunden auf Preiserhöhungen reagieren und setzen dementsprechend höhere oder niedrigere Preise
  • Elastizitäten geben an, wie sich eine Größe prozentual verändert, wenn wir eine andere prozentual erhöhen
  • in unserem Fall ist die  Preiselastizität der Nachfrage nach Gut 1

\[ \varepsilon_{X_1,p_1} \equiv \frac{\frac{\partial X_1(p_1)}{X_1(p_1)}*100}{\frac{\partial p_1}{p_1}*100} = \frac{\partial X_1(p_1)}{\partial p_1} \frac{p_1}{X_1(p_1)} \]



Teamarbeit: Gehen Sie zum Markt Widget und verändern Sie die Nachfrageparameter so, dass die Nachfrage elastischer wird!

Beispiel: Nachfrage mit konstanter Preiselastizität

Nehmen wir Cobb-Douglas Präferenzen mit Nachfragefunktion

\[ X_i = \frac{\alpha_i \ m}{p_i} \]

Dann ist die Preiselastizität

\[ \varepsilon_{X_i,p_i} = \frac{\partial X_i(p_i)}{\partial p_i} \frac{p_i}{X_i(p_i)} = \frac{-\alpha_i \ m}{p_i^2} \frac{p_i^2}{\alpha_i \ m} = -1 \]

Cobb-Douglas Präferenzen erzeugen Constant Elasticity of Substitution (CES) Nachfrage

  • Konsument:innen reduzieren ihre Nachfrage immer um ein Prozent, wenn der Preis um ein Prozent steigt

  • CES Präferenzen werden extrem häufig eingesetzt, da sie sehr angenehme Eigenschaften haben

Die Einkommenselastizität

Analog können wir die Einkommenselastizität von Gütern definieren:

\[ \varepsilon_{x_i,m} \equiv \frac{\partial x_i(p_i,m)}{\partial m} \frac{m}{x_i(p_i,m)} \]

Mithilfe dieser Elastizität können wir Güter nun formal kategorisieren

  • Normal: \(\varepsilon_{x_i,m}>0\)
  • Inferior: \(\varepsilon_{x_i,m}<0\)
  • Luxus: \(\varepsilon_{x_i,m}>1\)
  • Notwendige Güter: \(0<\varepsilon_{x_i,m}<1\)

Beispiel: Nachfrage mit konstanter Einkommenselastizität

Wiederum mit Cobb-Douglas Präferenzen und Nachfragefunktion

\[ x_i = \frac{\alpha_i \ m}{p_i} \]

haben wir

\[ \varepsilon_{x_i,m} = \frac{\alpha_i}{p_i} \frac{m}{\frac{\alpha_i \ m}{p_i}} = 1 \]

Jede Einkommenserhöhung um ein Prozent erhöht die Nachfrage nach jedem Gut um ein Prozent

  • Die Engel-Kurve ist eine Gerade mit Steigung \(\alpha_i/p_i\)

  • Diese Präferenzen sind daher homothetisch: die relativen Nachfragen sind unabhängig vom Einkommen

Die Konsumentenrente

Die inverse Marktnachfrage gibt an, welchen Preis Konsument:innen maximal bereit sind zu zahlen, wenn sie eine bestimmte Menge erwerben wollen – diesen Preis nennt man Reservations- oder  Vorbehaltspreis

  • Er korrespondiert mit einem bestimmten Nutzenniveau

  • Üblicherweise zeichnen wir die inverse Nachfragefunktion in unseren Diagrammen

Der gezahlte Preis entspricht einem bestimmten Nutzenverlust, da andere Güter mit dem verausgabten Geld nicht mehr erworben werden können

Die Konsumentenrente, ein Maß für die Wohlfahrt der Konsumentenseite, kann also über die Differenz zwischen inverser Nachfrage und dem Preis ermittelt werden

  • Steigt der Preis, fallen manche Konsumenten aus dem Markt und die Verbliebenen erfahren Nutzeneinbußen

Dieses zentrale Konzept werden wir für die Analyse von Steuern, aber auch von Marktversagen brauchen!

Zur grafischen Illustration geht es hier

Wiederholungsfragen

  • Erläutern Sie, welche Güterbündel sich Nachfrager überhaupt leisten können und von welchen Determinanten diese Menge abhängt

  • Gehen Sie alle Nutzenfunktionen anhand der interaktiven Grafik durch und erläutern Sie, warum die Indifferenzkurven die jeweilige Form annehmen

  • Wie findet man die optimale Nachfrage? Welche Herangehensweisen gibt es?

  • Nehmen Sie eine bestimmte Klasse von Nutzenfunktionen und versuchen Sie, mithilfe einer interaktiven Grafik Einkommens-Expansionspfade, Engel-Kurven und Nachfragefunktionen zu konstruieren

  • Suchen Sie sich einen Partner und erklären dieser Person die Begriffe „Preiselastizität“, „Einkommenselastizität“ und „Konsumentenrente“

Widgets

Nutzenmaximierung

Formel
f
Budget
Indifferenzkurven

Zurück zu „Budget“, „Indifferenzkurven“, „Optimale Nachfrage“, „Einkommen“ oder „Preise“

Markt

Zurück zu “Preiselastizität oder „Konsumentenrente“